- 1
- 2
Initiation au jeu de Nim
J’ai envie de débuter une série d’articles sur la théorie des jeux. C’est un domaine particulièrement intéressant des mathématiques et surement un des plus ludiques. Je vous propose de démarrer par une catégorie extrêmement simple de jeux qu’on appelle couramment les jeux de Nim.
Pour ceux qui l’ignorent, les jeux de Nim sont une catégorie de jeux où deux joueurs s’affrontent au tour par tour et qui consistent à prendre ou déplacer des objets en respectant certaines règles pour passer d’un état à un autre (sans avoir la capacité de revenir à un état précédent) jusqu’à atteindre une position de victoire. Cela a l’air assez flou comme ça, n’est-ce pas ? C’est normal, c’est une définition générique car les jeux de Nim englobent un nombre de jeux assez large même si derrière, il y a toujours la même logique. Un des jeux de Nim les plus connus a été rendu populaire à notre époque par une épreuve de Fort Boyard, celle des bâtonnets. Deux joueurs ont devant eux un plateau où se tient un certain nombre de bâtonnets. À chaque tour, le joueur a la capacité de retirer un, deux ou trois bâtonnets. Celui qui retire le dernier bâtonnet a perdu. Ceci est un jeu de Nim, on a deux joueurs qui alternent, chacun peut retirer un certain nombre d’objets fixé par les règles initiales et on arrive à une situation finale qui est de vider le plateau tout en sachant que celui qui prend le dernier perd. En outre, il est impossible de retourner à un état précédent car on ne peut que retirer des bâtonnets. À l’inverse, les échecs par exemple ne sont pas un jeu de Nim car on peut totalement revenir à une position antécédente. Par exemple, je bouge mon cavalier, mon adversaire fait de même puis je remets mon cavalier à sa place initiale et mon adversaire fait de même. Ici, on vient de passer d’un état de l’échiquier à un autre strictement identique. Cela signifie que tout ce qu’on va voir pour être sûr de gagner dans un jeu de Nim ne peut pas s’appliquer dans un jeu d’échec.
Je me dois également de préciser certaines caractéristiques inhérentes au jeu de Nim. Il n’y a pas, dans un jeu de Nim, de notion de hasard. Si je prends l’ensemble des jeux avec des dés par exemple, tel que les petits chevaux, ce ne sont pas des jeux de Nim. C’est également un jeu qui se doit d’avoir ce qu’on appelle des informations complètes et parfaites. Cela signifie qu’on connait exactement l’ensemble des variables qui constituent le jeu. Dans mon jeu des bâtonnets, je vois combien de bâtonnets au total et je sais combien moi et mon adversaire avons la capacité de retirer. À l’inverse, la plupart des jeux de cartes ne sont pas des jeux de Nim tel que le Black Jack ou le Poker car nos informations ne sont pas complètes et parfaites tant on ignore la main de nos adversaires. Là encore, pour ces jeux, c’est d’autres stratégies qu’il va falloir adopter que celle du jeu de Nim. Enfin, un jeu de Nim est un jeu à somme nulle. Cela signifie que si je gagne une manche alors l’autre joueur en perd obligatoire une. Il n’y pas de situations où tout le monde est vainqueur ou perdant. Vous notez que tout ça est assez restrictif mais c’est normal, on a dit qu’on commençait simple. On ne va pas se lancer dans des probabilités ou des graphes à circuits.
Dans tout jeu de Nim, la stratégie est la suivante. La phase la plus complexe est la première, il va falloir lister l’ensemble de tous les états possibles du jeu. En un sens, ce n’est pas difficile, c’est juste long et rébarbatif. Après, on a des ordinateurs pour faire ça maintenant. Ensuite, on tisse les liens qui, en fonction des règles, nous permette de passer d’un état à l’autre. Imaginons dans notre jeu des bâtonnets (qui se fait très bien avec des allumettes aussi), on commence avec 12 éléments alignés. On a donc une liste décroissante de 12 à 1 et comme on peut retirer un, deux ou trois à chaque tour, alors chaque élément est lié à son élément-1, élément-2 et élément-3. Cela nous donne le graphe orienté suivant :
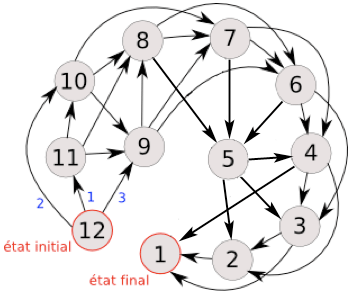
Une fois le graphe fait, vous venez de faire le plus dur du travail. Maintenant, il faut déterminer les états finaux. Dans le cas de notre jeu de bâtonnets, il n’y en a qu’un. C’est quand il en reste plus qu’un. En effet, si on arrive à la fin de notre tour au cas où il n’en reste plus qu’un, on a gagné car l’autre n’a d’autre choix que de le retirer. Mais dans d’autres jeux de Nim, il peut y avoir plusieurs états gagnants. Le but est de les répertorier. À partir de là, on va voir tous les états qui pointent sur eux. Dans notre cas, par exemple, on a le 2, 3 et 4. Ces cas sont considérés comme perdants. Pourquoi ? Car si à la fin de votre tour, vous atterrissez sur un de ces états, votre adversaire peut atteindre la position gagnante et donc vous perdez. On ne veut pas ça. Par contre, c’est tout le sort qu’on souhaite à notre adversaire. C’est pour ça que nous allons chercher un état qui ne mène qu’à des états perdants. Est-ce qu’on a cela ? 5 mène à 2, 3 et 4 qui sont tous perdants. Ainsi, si j’arrivais sur 5, mon adversaire n’aurait d’autres possibilités que de venir sur un état perdant. On dit que 5 est un état gagnant. Et comme 5 est un état gagnant, on reproduit le même processus qu’avec 1. Les états qui pointent dessus sont déclarés perdants et on cherche un état qui pointe que sur des perdants. Il devient un nouveau gagnant et on continue jusqu’à arriver à l’état initial. Ces éléments gagnant sont appelés noyaux. Dans notre cas, on arrive au résultat suivant :
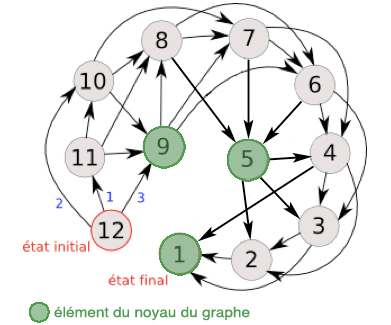
Comme notre logique est bien faite, on note que les éléments du noyau peuvent être tous atteint en deux tours. C’est trivial vu que les perdants pointent forcément sur un gagnant et qu’un gagnant ne pointe que sur des perdants. Ainsi, si à la fin de votre tour, vous arrivez sur une situation gagnante, alors vous êtes sûr de gagner si vous jouez bien. Votre adversaire n’ayant pas le choix de tomber sur un cas perdant, vous devrez alors rejoindre le prochain cas gagnant. Si votre êtes sur 9 et que votre adversaire en retire 3 et atterrit donc sur 6, n’allez pas sur 4 mais sur 5. De même, si vous commencez, allez vite en 9 en en retirant 3.
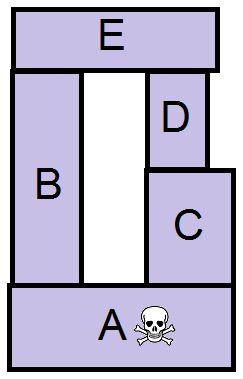
Ainsi, les jeux de Nim ne sont guère intéressants si on joue avec des personnes éclairées car dès le début, vous pouvez savoir qui a gagné ou perdu. Je prends par exemple, le morpion ou tic-tac-toe, je pense qu’on y a tous joué étant enfant. Une fois qu’on sait bien y jouer, au bout du second coup, on sait si on gagne ou si on fait un match nul (si le joueur joue bien, car sinon, il peut commettre des erreurs et on peut les exploiter pour gagner). Après, bien que déterminable, on ne s’amuse pas toujours à calculer les noyaux d’un graphe dans notre tête. Car créer le graphe peut s’avérer parfois complexe bien que possible. Par exemple, si je prends le puissance 4, le nombre de configuration possible est énorme. Mais on peut le faire (ce qui me permet de vous dire que si deux joueurs jouent parfaitement au puissance 4, si le premier joueur met son pion au milieu, il est assuré de gagner et à l'inverse s'il le met sur les extrémités, il est assuré de perdre). Malgré tout, sur les Nim, cette stratégie marche toujours. Je vous laisse l’essayer sur ce petit jeu. Vous et votre adversaire vous retrouvez devant cette pile. À chaque tour, vous devez retirer un morceau. Attention toutefois, Si vous prenez une pièce, vous êtes obligé de prendre toutes les pièces qui sont au-dessus de celle-ci. Celui qui prend le dernier morceau avec le crane a perdu. Vous débutez, quelle pièce devez-vous prendre ?
Parlons de sommes
Si vous êtes venus en espérant dormir (faire un petit somme), hélas, il y a méprise. Dans cet article, on va parler méthodes de sommations. En gros, on va additionner des trucs. Trivial me direz-vous. En êtes-vous vraiment bien sûr? Si cela peut sembler trivial en effet, c'est quand même un sujet assez profond que je me dois d'aborder. Je vais tâcher évidemment de rester le plus accessible possible. Mais si vous venez en pensant que cela sera une sinécure, à moins d'avoir un bon niveau de base en mathématique, vous vous tournerez vers vos successeurs et vous leur direz :

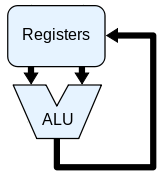
"Sincèrement, pourquoi une telle mise en garde pour de bêtes additions". Tu verras, Billie, tu verras. Commençons donc par définir ce qu'est une sommation. La sommation est une fonction qui prend un nombre variable de paramètres et qui va vous ressortir le résultat des additions successives. Appelons la S. Si je fais S(4,5) alors ça va me sortir le résultat de l'addition 4+5 soit 9. Jusque là, je ne pense pas vous avoir largué. Je tiens à faire le distinguo entre la sommation et l'addition. La sommation est une succession d'additions comme je l'ai dit. L'addition, elle, n'est qu'une opération arithmétique qui prend deux grandeurs (ça peut être des nombres mais ça peut être tout, comme des longueurs, des pommes, etc.). Et en réalité, je tiens à insister sur DEUX grandeurs. Si je vous demande S(3,4,5), je demande donc le résultat du calcul suivant : 3+4+5. Je peux placer mes parenthèse comme je veux grâce à l'associativité mais dans tous les cas, que je fasse (3+4)+5 ou 3+(4+5), je vais nécessiter 2 additions. On fait notre première opération (3+4) ou (4+5) et on réinjecte le résultat comme autre entrée pour la prochaine addition. C'est comme cela que procède vos calculatrices et vos ordinateurs. Ils ont une unité arithmétique et logique (UAL ou ALU en anglais) qui prend 2 entrées et donne une seule sortie qui peut potentiellement servir d'entrée pour le prochain calcul.
Jusque là, ça va, je n'ai pas cassé trois pattes à un canard. Continuons donc. Vous êtes vous déjà demandé quelles propriétés se doit d'avoir une fonction de sommation? Car là, je vous ai présenté la basique qui se contente de faire des additions successives mais il y en a bien d'autres comme nous le verrons par la suite. Il doit donc bien y avoir des critères pour dire qu'une fonction de sommation est valide mathématiquement. Cela se tient dans le triptyque Métro-Boulot-Dodo, heu, linéarité-stabilité-régularité. Qu'est-ce qui en retourne?
La linéarité, c'est simple. Cela signifie que je conserve la même proportionnalité en faisant des manipulations arithmétiques élémentaires sur ma sommation. Je m'explique. Prenons le calcul suivant : 3+4+5, cela me donne comme somme 12 évidemment. Si je multiplie chacun de mes éléments par 2 alors ma somme doit également être multipliée par deux pour conserver la même proportion. Je vérifie, 6 + 8 + 10, cela me donne bien 24, soit 2 fois le résultat initial. Donc pour tout nombre lambda, j'ai : [math]\sum_{n=1}^{m}(\lambda \times a_n) = \lambda \times \sum_{n=1}^{m}a_n[/math]. Si vous n'êtes pas familier avec ce type de notation, sachez que [math]\sum_{n=1}^{m}[/math] signifie la somme de n=1 jusqu'à une valeur "m" et [math]a_n[/math] est le paramètre de ma sommation en position n. Donc pour l'exemple S(3,4,5) = 3+4+5, je peux l'écrire [math]\sum_{n=1}^{3}a_n[/math] et j'aurai alors additionné les 3 paramètres dans l'ordre 1,2 et 3 qui valent successivement 3, 4 et 5. Cela revient bien au même.
Mais ce n'est pas tout, si j'ai une autre somme, tel que 0+1+2 qui me donne 3. Si je l'additionne deux à deux avec ma sommation précédente, alors je dois avoir l'addition des deux sommes. En somme (haha), ça revient à dire que si je fais (3+0)+(4+1)+(5+2) alors c'est censé me donner l'addition des sommes, soit 12+3 donc 15. Et si je regarde, c'est bien ce que j'ai  (notez que si vous n'avez pas le même nombre d'éléments, vous faites comme moi, vous ajoutez des 0 dans la sommation qui en a le moins). De là, on peut dire que [math]\sum_{n=1}^{m}a_n + \sum_{n=1}^{m}b_n= \sum_{n=1}^{m}(a_n +b_n)[/math].
(notez que si vous n'avez pas le même nombre d'éléments, vous faites comme moi, vous ajoutez des 0 dans la sommation qui en a le moins). De là, on peut dire que [math]\sum_{n=1}^{m}a_n + \sum_{n=1}^{m}b_n= \sum_{n=1}^{m}(a_n +b_n)[/math].
Ainsi, on est capable de déterminer une formule de la linéarité pour la sommation. Votre fonction de sommation est linéaire si l'égalité suivante est vraie :
[math]\lambda \times \sum_{n=1}^{m}a_n + \beta \times \sum_{n=1}^{m}b_n= \sum_{n=m}^{n}(\lambda \times a_n + \beta \times b_n)[/math].
Une fonction de sommation est dite stable si je peux en extraire ces n premiers nombres et les additionner naturellement à la fonction de sommation débutant désormais aux n+1-ème nombres. Qu'est-ce que ce charabia? En réalité, ça veut juste que si je fais S(1,2,3,4,5,6), j'aurai le même résultat que si je fais 1+2+3+S(4,5,6). Le fait que je sorte certains termes de la fonction de sommation pour les additionner de manière traditionnelle est indolore et ne change strictement rien. De même, l'autre sens est également possible. Si 1+2+3+S(4,5,6) alors, il faut que j'obtiens la même somme que si j'avais S(1,2,3,4,5,6). Forcément, ça découle de ce qu'on a vu en début de paragraphe et ça a l'air induit comme ça. Précisons également que ça marche même si on n'a pas de terme à gauche (en gros, si on a des 0). [math]S(1,2,3) = 0 + S(1,2,3) = S(0,1,2,3)[/math].
De facto, on peut résumer en disant que notre fonction est stable si, pour une série de nombres [math]a_n[/math], on a [math]\sum_{n=1}^m a_n = a_1 + a_2 + a_3 + \sum_{n=4}^m a_n[/math]
On peut utiliser toutes les méthodes de sommation qu'on souhaite mais pour des opérations qu'on connaît, elles doivent impérativement donner le même résultat que la méthode d'addition usuelle. Et ça parait, de vous à moi, logique. Je peux développer une superbe fonction de sommation mais si 1+1 = 3, j'ai un sérieux problème. Cela a l'air extrêmement bateau de dire ça mais c'est quand même une prémisse indispensable.
En tout cas, voilà ce qu'il vous faut impérativement pour avoir une fonction de sommation correcte. Si vous ne l'avez pas alors vous risquerez d'arriver à des résultats faux. Donc voilà, c'est important à garder en tête. Mais attention, un résultat qui peut sembler aberrant n'est pas forcément faux, non plus. On verra ça plus tard.
"C'est mignon tout ça mais franchement, tu te fais ch***. Pourquoi tant se prendre la tête pour une simple addition en masse? C'est comme, pourquoi tu t'évertue à mettre ça sous forme de fonction S alors que des + font très bien l'affaire? Tss, ces mathématiciens, ça aime se compliquer la vie pour des choses simples".
Tient, Billie reprend du poil de la bête. C'est vrai que dans les additions bateaux comme celles dont on a fait mention ci-dessus, cela fait très superflu. Mais déjà, cela permet de formaliser les choses et d'avoir ainsi une base solide et surtout vous allez voir que les additions, ce n'est pas toujours si simple. Surtout lorsqu'on va vers l'infini  . Vous le sentiez venir, n'est-ce pas? Car après tout, comment comptes-tu faire, Billie, pour me calculer la somme suivante : [math]\sum_{n=1}^{\infty} \frac{9}{10^n}[/math] soit [math]0.9+0.09+0.009+...[/math]? Hé bien avec la méthode de sommation actuelle, ce n'est plus possible. En effet, on ne peut pas sortir une somme d'une succession infinie avec notre simple opérateur +. Il a atteint ses limites haha
. Vous le sentiez venir, n'est-ce pas? Car après tout, comment comptes-tu faire, Billie, pour me calculer la somme suivante : [math]\sum_{n=1}^{\infty} \frac{9}{10^n}[/math] soit [math]0.9+0.09+0.009+...[/math]? Hé bien avec la méthode de sommation actuelle, ce n'est plus possible. En effet, on ne peut pas sortir une somme d'une succession infinie avec notre simple opérateur +. Il a atteint ses limites haha  (vous comprendrez bientôt pourquoi c'est drôle). Il va donc falloir changer de fonction de sommation. Et là, plein de possibilités s'offrent à nous. Et il va alors faire un choix.
(vous comprendrez bientôt pourquoi c'est drôle). Il va donc falloir changer de fonction de sommation. Et là, plein de possibilités s'offrent à nous. Et il va alors faire un choix.
La méthode traditionnelle est de regarder la limite des sommes partielles de notre sommation infinie. Ainsi, notre fonction de sommation S devient dans le cadre d'une sommation infini : [math]S = \lim\limits_{n \rightarrow +\infty}(a_1+a_2+a_3+...+a_n)[/math]. Car en effet, autant notre sommation ne s'arrête jamais, autant elle peut se rapprocher de plus en plus d'une valeur déterminable. On dit alors que cette somme converge vers une valeur. Cette valeur n'est autre que la limite (en l'infini) des sommes partielles de la sommation. Pour y voir plus clair, regardons l'exemple [math]\sum_{n=1}^{\infty} \frac{9}{10^n}[/math] et notamment ses sommes partielles. À la première itération, on a 0.9, à la seconde 0.99, à la suivante 0.999 et ainsi de suite. On voit bien que cette série se rapproche de plus en plus près de 1 qui est la plus proche valeur qu'elle ne dépassera jamais de façon certaine. 1 est la limite de cette suite. Mais du coup, si vous vous rapprochez infiniment d'une valeur, ne peut-on pas dire que vous êtes cette valeur. "Non! Il y aura toujours un écart même infime!". Vraiment? Je parle ici de l'infini. Il n'y aura jamais un 9 final donc peut-il y avoir un écart. Faut voir ça autrement. Imaginons, je te suis, Billie. Il y a un écart. Dans ce cas là, combien dois-je enlever à 1 pour avoir la valeur de ma somme? 0.1? 0.0000001? Il faudrait retirer 0.000000... et ça n'aura jamais de fin car il y aura toujours un 9 après le 9. Si au final, je dois retirer une infinité de 0 à 1 pour que ça soit également à ma somme, en réalité, je ne dois rien retirer. Et donc 1 serait bien égale à 0.99999999... Comme je vous l'avais annoncé dans mon précédent article, c'est fou  .
.
Pour votre curiosité personnelle, on peut aisément montrer que la suite tend vers 1. On a une suite géométrique de première terme [math]u_o = \frac{9}{10}[/math] et de raison [math]q = \frac{1}{10}[/math]. On sait que la somme des termes d'une suite géométrique s'obtient en calculant [math]u_0 \times \frac{1-q^{n+1}}{1-q}[/math]. Dans notre cas, on a donc : [math]\frac{9}{10} \times \frac{1-(\frac{1}{10})^{n+1}}{1-\frac{1}{10}} = \frac{9}{10} \times \frac{1-\frac{1}{10^{n+1}}}{\frac{9}{10}} = 1-\frac{1}{10^{n+1}}[/math]. Or [math]\lim\limits_{n \rightarrow +\infty}\frac{1}{10^{n+1}} = 0 \Rightarrow \lim\limits_{n \rightarrow +\infty}1 - \frac{1}{10^{n+1}} = 1 [/math]
Cette méthode marche parfaitement pour toute somme absolument convergente. Et j'insiste sur le mot "absolument". Pour clarifier davantage, dans notre somme, il n'y a pas une alternance de signe qui prise isolément diverge vers l'infini. Prenons un exemple, la formule de calcul de Pi découverte par Madhava de Sangamagram en est un excellent. Il a réussi à démontrer que [math]\pi = 4 - \frac{4}{3} + \frac{4}{5} - \frac{4}{7} + \frac{4}{9} - ...[/math]. Et cette somme [math]4 \sum^{\infty}_{n=0} \frac{(-1)^n}{2n+1}[/math] converge vraiment vers pi. Mais regardons la suite formée uniquement par les termes positifs. On a [math]4 + \frac{4}{5} + \frac{4}{9} + + \frac{4}{13} + ...[/math]. On peut le démontrer mais l'article est déjà long donc je vous prie de me croire sur parole, cette série diverge vers [math]+\infty[/math]. Regardons maintenant la suite faite par les nombres négatifs, on a : [math]- \frac{4}{3} - \frac{4}{7} - \frac{4}{11} -...[/math] et là encore, croyez moi, ça diverge vers [math]-\infty[/math]. On parle alors de série semi-convergente.
Vient alors un problème. En réordonnant les nombres de cette série, comme elle marche par compensation pour converger, je suis capable de la faire converger vers n'importe quel nombre. C'est ce qu'on appelle le théorème de réarrangement de Riemann. Il s'explique extrêmement facilement. Prenez votre série et faites en deux listes ordonnées, l'une avec les nombres positifs du plus grand au plus petit et l'autre avec les nombres négatifs du plus grand au plus petite. Choisissez alors le nombre vers lequel vous voulez converger. Dépilez et additionnez autant de nombres positifs nécessaires de votre liste jusqu'à dépasser votre nombre. Une fois dépassé, vous dépilez et additionnez autant de nombres négatifs nécessaires de votre seconde liste jusqu'à être en dessous de votre nombre. À partir de là, vous continuez le processus. Comme vos listes sont triées, à chaque fois, vous vous rapprocherez irrémédiablement et à l'infini de votre valeur voulue. Félicitation, vous venez de faire converger votre série là où vous le souhaitez. Reprenons la formule de calcul de pi. En la réarrangeant un petit peu, on a [math]4 - \frac{4}{3} - \frac{4}{7} - \frac{4}{11} - \frac{4}{15} + \frac{4}{5} - \frac{4}{19} - ...[/math] qui converge alors vers le nombre d'or.
De facto, notre méthode de calcul de somme infini marche bien mais on perd une fonction de notre système d'addition lors d'une série semi-convergente. On ne peut plus toucher à l'ordre des termes. On perd donc la propriété de commutativité de l'addition. Pour ceux qui l'ignorent, la commutativité est ce qui nous permet d'affirmer que 1+2+3 est strictement égal à 3+1+2. On peut réarranger nos nombres, cela ne change rien. Alors la sommation usuelle de série semi-convergente, ce n'est hélas plus possible.
Vous vous doutiez bien que depuis on a trouvé des outils pour les séries divergentes. Pour cela, il vous suffit de changer de fonction de sommation. En réalité, si vous lisez mes articles assidument, vous devez déjà en connaître une, on l'a vu dans l'article "1-1+1-1+1-1+...=1/2" et se nomme la sommation de Cesàro. Cette fonction de sommation s'intéresse plus à la simple limite des sommes partielles mais à la limite de la moyenne des sommes partielles, c'est-à-dire : [math]S = \lim\limits_{n \rightarrow +\infty}\frac{1}{n}(a_1+a_2+a_3+...+a_n)[/math]. Je vous laisserai vérifier qu'elle respecte les trois propriétés mentionnées ci-dessus (linéarité, stabilité et régularité), vous êtes grand. En réalité, c'est bien car la sommation de Cesàro est "valide" qu'on peut faire le raisonnement suivant :
[math]S = 1-1+1-1+1-1+…\\
\Rightarrow 1-S = 1- (1-1+1-1+1-1+…)\\
\Rightarrow 1 – S = 1-1+1-1+1-1+…. \\
\Rightarrow 1- S = S\\
\Rightarrow 2S = 1\\
\Rightarrow S = \frac{1}{2}[/math]
Alors évidemment, une somme infinie de 1 et de -1 donnant [math]\frac{1}{2}[/math], ça a de quoi surprendre. Mais je me permettrai de citer mon article :
~Yann Bidon
L'infini est plein de surprises, croyez-moi. Il nous force à sortir de notre cadre conventionnel pour ouvrir à de nouvelles perspectives. On peut le rejeter, nier l'infini. Pourtant, ces calculs aux résultats surprenants trouvent étonnamment des applications des plus concrètes, notamment en physique, preuve de leur véracité. Sachez que d'autres méthodes de sommation existent tels que celles d'Abel, de Borel... Je ne vais pas toutes les lister. Peut-être feront-elles l'objet d'un autre article mais pour l'heure, notez qu'en cas de divergences, on a des outils mathématiques pour nous aider.
"Donc toute sommation a un résultat définissable?" Non, Billie. J'en suis navré mais malgré tous nos outils, on ne peut parfois pas trouver de résultats. Prenons la somme [math]S = \sum 1 = 1+1+1+1+...[/math]. Que se passe-t-il si j'applique la même logique de celle de la série de Grandi?
[math]S = 1+1+1+1+1+1+…\\
\Rightarrow 1+S = 1+ (1+1+1+1+1+1+…)\\
\Rightarrow 1+S = 1+1+1+1+1+1+…\\
\Rightarrow 1+S = S\\
\Rightarrow 0 = 1[/math]
En cela, tu notes bien qu'on a ici un raisonnement par l'absurde témoignant de la non-linéarité du procédé et donc qu'on n'a pas de fonctions linéaires, stables et régulières qui nous permettraient d'obtenir un résultat. Ca va juste vers l'infini, point.
"Objection! Wiki, il a dit que c'est possible et que ça vaut [math]- \frac{1}{2}[/math]". Je comprends tout à fait ton objection. Et c'est bien de garder l'esprit ouvert et de diversifier tes sources. Mais que dit exactement l'article de Wiki? Il ne parle pas de somme, il parle d'une régularisation. C'est un autre procédé mais je ne vais pas le détailler ici. Mais vu que tu aimes wiki, clique ici pour allait voir la page associée.
Bon, je vais m'arrêter là, je pense. Mais comme vous voyez, cette initiation à la sommation infinie fut quand même bien consistante  . J'espère avoir su rester le plus didactique possible et que je ne vous ai pas trop larguer. Sinon, bah voyez l'image de début d'article
. J'espère avoir su rester le plus didactique possible et que je ne vous ai pas trop larguer. Sinon, bah voyez l'image de début d'article  .
.
Qu'est-ce que l'infini?
Il est 23h à l'heure où je commence à écrire ces lignes, nous sommes le 24 décembre 2016 et voilà que je ne trouve rien de mieux que de débuter un article sur un des sujets qui n'est pas forcément le plus complexe mais un des plus abstraits des mathématiques : l'infini. Vaste sujet que voici, ainsi, comprenez bien qu'un seul article ne me suffira pas pour couvrir le système. C'est un sujet également passionnant car à l'instar des voyages dans le temps, cela reste totalement conceptuelle à ce jour et amène son lot de paradoxe en tout genre. C'est une intense réflexion philosophique et mathématique. Mais pour le moment, commençons tout en douceur avec une définition de l'infini. Qu'est-ce que l'infini?
On va commencer si vous le souhaitez bien par l'antagoniste et donc le "fini". On dit qu'un ensemble est fini lorsqu'il est possible de compter les éléments de cet ensemble sans omission ni répétition et ainsi d'en déduire ce qu'on appelle sa cardinalité, c'est-à-dire le taille de cet ensemble, et que ce dernier soit un nombre entier. Par exemple, les chiffres sont dénombrables. Ils ont une cardinalité de 10, c'est l'ensemble {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Je suis capable de les compter et d'en sortir un nombre entier (ici, 10). Le nombre d'humain sur Terre à cet instant précis est un ensemble fini. Cela va me prendre un temps énorme à tous les recenser mais j'en ai la capacité. Le nombre de graine de sable sur cette planète est un ensemble fini. Il sera très loin et impossible en une seule vie, seule, de tous les compter un à un (et qu'est-ce que cela serait chiant) mais cela reste dans le domaine du possible. Je peux tous les répertorier, un à un et les indexer avec un nombre entier croissant. J'arrivera alors à une fin.
Avant d'attaquer le cœur du sujet, j'aimera aborder un autre point : la bijection. Lorsque deux ensembles ont une cardinalité identique, alors nous sommes capable de faire une bijection. C'est-à-dire qu'on est capable de coupler deux à deux chaque élément d'un ensemble alors un élément de l'autre ensemble et n'obtenir aucun reste ni aucun manque. Je m'explique. Imaginez que vous avez un ensemble de chaises et un ensemble de personnes. Il y a bijection si vous êtes capable de mettre chaque personne sur une chaise et qu'à la fin, il n'y a ni chaise vide ni personne debout. A chaque chaise, vous êtes arrivé à faire correspondre une personne. Si vous êtes capable de faire une bijection alors veut dire que les deux ensembles ont la même cardinalité. Si je prends un autre exemple plus mathématique alors imaginons l'ensemble {1,2,3} et l'ensemble {2,4,6}, je suis capable de lier un à un les éléments et c'est normal car vous notez que j'ai juste multiplié par 2. Cette opération de multiplier par 2 est bijective car elle touche en rien la cardinalité de l'ensemble. Gardez ça dans un coin de votre tête  .
.
Bien, c'est bien beau tout ça, mais le sujet est l'infini et non le fini. Alors qu'est-ce que l'infini? Je t'écoute Billie: "Hé bien, si je garde en tête tous ce que tu as dit précédemment, c'est quelque chose qu'on ne peut pas compter". Arf, ce n'est pas si simple Billie. Car vois-tu, il y a plusieurs types d'infini. En réalité, il y a même une infinité d'infinis. Et tous ne se valent pas. Parmi cette infinité d'infinis, il y a un ensemble qui est celui des infinis dénombrables, c'est-à-dire des infinis qu'on peut compter. En effet, j'ai bien fait la précision plus haut, pour qu'un ensemble soit fini, il faut qu'on puise lister sans omission ni répétition les éléments via un index de nombre entier et arriver à une cardinalité entière. Le point crucial est cette dernière partie. Car il y a des ensembles que je peux indexer. C'est le cas notamment de l'ensemble des entiers naturels. On est d'accord que cet ensemble est infini. Pour tous nombres de cet ensemble, je suis toujours capable d'en trouver un autre en ajoutant 1 et ce, continuellement. Pourtant, je suis capable de les compter. Chaque nombre de cet ensemble correspond à un numéro, un index qui équivaut lui-même +1 (à cause du 0 qui occupe la première position). Si on me demande où se trouve un gogol ([math]10^{100}[/math]), je lui dirai en gogol+1 position. Je suis capable de les compter, simplement, il a une cardinalité [math]\infty[/math](symbole de l'infini). Et là, vous allez me dire, c'est assez intuitif, le cas des entiers naturels est assez simple. Et c'est vrai mais sachez par exemple que l'ensemble des rationnels positifs est dénombrable. L'image ci-dessous montre qu'il est possible d'ordonner et donc compter l'ensemble infini des fractions positives:

"Ok, ok, laisse-moi retenter alors. Un ensemble est dit infini si sa cardinalité est l'infini". Ma remarque de tout à l'heure visait à souligner l'existence d'ensemble infini dénombrable (et donc avec une cardinalité infini). Cependant, tous ne le sont pas, ainsi, je ne peux accepter cette définition réductrice, Billie, désolé. Regarde, l'ensemble des réels ne peut être compté. Tu commences par 0 puis ensuite quoi? 0.000001? Mais tu as 0.0000001 avant voire même 0.00000...1. Mes honorés lecteurs, vous allez me rétorquer que cet argument ne suffit pas à monter qu'on ne peut les compter. Peut-être en effet existerait-il une méthode spéciale à l'instar de ce qu'on a fait avec les rationnels. Très juste, hélas, il a été démontré par Cantor en 1891 qu'on ne pouvait les dénombres via l'argument de la diagonale. Puisqu'on ne peut les dénombrer, prenons des nombres infinis au hazard. En partant du premier élément, je trace une diagonale. Je tombe alors sur un chiffre à chaque ligne. Je vais alors reconstituer un nombre en incrémentant de un chaque chiffre et en passant le 9 à 0. Ce nombre sera forcément nouveau car il différera forcément d'un chiffre par rapport à un nombre précédent. Rien ne vaut une image:

Vous allez me rétorquer "mais du coup, on peut les indexer". Bah non car pour déterminer le nombre, on a besoin de la diagonale en entière et donc de la liste déjà formée. Ce qui est impossible car infini donc conceptuellement, on sait qu'ils sont infinis mais on sait qu'on ne peut les compter.
"Bon ok, l'infini, c'est la taille d'un ensemble dont la cardinalité n'existe pas ou n'est pas entière. Ca te va mieux?" Il y a du mieux. Vraiment. Mais j'aimerai qu'on insiste davantage sur le fait que l'infini n'est pas un nombre. C'est un concept, comme Dieu, la Destinée, l'origine de tout. Cela permet de traiter un sujet difficilement matérialisable, palpable et au final, dont on ne sait pas grand chose. C'est un label, une étiquette qu'on met pour désigner une caractéristique, ce n'est pas quelque chose de figer. Si je prends un ensemble infini, alors si j'ajoute un élément, j'aurai toujours un ensemble infini, ça veut dire que [math]\infty + 1 = \infty[/math]. Ca n'a pas de sens mathématiquement parlant. L'infini n'est pas un nombre, on n'additionne pas des choses à l'infini. Mais sortons des nombres pour un exemple plus concret. Connaissez-vous l'hôtel de Hilbert? C'est un hôtel imaginaire qui a la particularité d'avoir une infinité de chambres. Imaginons que cette infinité de chambre soit occupé par une infinité de client. Vous vous présentez à l'accueil, pourrons-t-il vous accueillir? Oui. Car contrairement à un ensemble fini, on a ici une infinité de chambre et ce, même en présence d'une infinité de client. On va simplement faire une translation. On va demander à chacun des occupants d'aller dans la chambre dont le numéro est augmenté de 1 par rapport à la sienne. Donc le 1 ira dans le 2, le 2 dans le 3 et ce infiniment. Il y aura forcément une chambre avec le numéro d'après car c'est infini. Il ne vous reste plus qu'à occuper la chambre 1 désormais désertée.
Cela peut même aller à l'encontre de notre intuition. Prenez l'ensemble des entiers naturels {0, 1, 2, 3, ...} et l'ensemble {0, 2, 4, 6, ...}. Intuitivement, on dirait que le premier contient plus d'éléments que l'autre. Mais avec l'infini, ce n'est pas vrai. Ca ne change rien, cela reste l'infini. Et pour le prouver, je vais faire appel à la parenthèse de tout à l'heure, la bijection. Ici, j'ai de nouveau pris l'ensemble du double des entiers naturels. J'ai juste multiplié infiniment par 2. Donc je suis capable de les coupler un à un et donc de faire une bijection. De ce fait, ils font la même taille. Donc [math]2 \times \infty = \infty[/math]. Ils sont de même taille alors qu'intuitivement, on dirait que le premier en à plus. Si on reprend l'exemple de l'Hôtel de Hilbert, imaginons que cette fois, une nouvelle infinité de client se présente aux guichets, peut-on les accueillir? Oui, encore une fois, une simple translation suffit. On demande aux clients de prendre la chambre dont le numéro est le double du leur. Vous venez de libérer une infinité de chambres pour accueillir votre infinité de client.
De là, il faut juste retenir une chose. L'infini n'est pas un nombre, on ne fait pas d'opération dessus. C'est un concept. "Je vois. Mais dans ce cas, que voulais-tu dire tout à l'heure quand tu as dis que tous les infinis ne se valent pas? Car si les opérations ne changent rien à la nature de l'infini, qu'est-ce qui les distinguerait?" Certains infinis sont plus petits ou plus grand que d'autres. Mais cela sera l'occasion d'en parler dans un article Billie. Il se fait tard et je vais y aller. Bonne nuit Billie et joyeux Noël à mes chers lecteurs.
Expliquons ce tour de Fabien Olicard
Fabien Olicard est un mentaliste que je suis depuis un moment et j'ai même eu la chance de le voir en spectacle récemment à Lyon. Il a sorti une vidéo dans lequel il essaie de nous bluffer. C'est un tour mathématique donc forcément, l'impact sur moi fut moindre mais il est toutefois assez ludique et peut faire son effet sur les non-initiés. Je vous propose de le découvrir ici et j'expliquerai le tour plus en profondeur juste après:
Évidemment, vous n'aviez en réalité pas le choix. Vous ne pouviez tomber que sur "Logique". Pourquoi? Eh bien, c'est logique  . Il a utilisé la propriété des multiples de 9 dont j'ai parlé dans un précédent article. Pour tout multiple de 9 non nul, la somme successive des chiffres qui le compose aboutira inlassablement à 9. Et dans sa grille, si on regarde le positionnement du mot logique, on le trouve à la position 9, 18 et 27 (tous des multiples de 9). Sachant qu'une différence d'année restera dans le pire des cas à 4 chiffres, il avait anticipé que vous ne pourrez aller plus loin.
. Il a utilisé la propriété des multiples de 9 dont j'ai parlé dans un précédent article. Pour tout multiple de 9 non nul, la somme successive des chiffres qui le compose aboutira inlassablement à 9. Et dans sa grille, si on regarde le positionnement du mot logique, on le trouve à la position 9, 18 et 27 (tous des multiples de 9). Sachant qu'une différence d'année restera dans le pire des cas à 4 chiffres, il avait anticipé que vous ne pourrez aller plus loin.
Cependant, d'où sort le nombre 9? Après tout, il vous a demandé de prendre votre année de naissance. C'est propre à chacun. Et c'est vrai. Néanmoins, la manipulation qu'il vous demande de faire aboutira toujours au même résultat, ça donnera un multiple 9. Je m'explique. Prenons un nombre quelconque en base 10 sur 4 chiffres : [math]a \times 1000+b \times 100+c \times 10+d[/math]. Si on inverse l'ordre des chiffres, on obtient alors [math]d \times 1000+c \times 100+b \times 10+a[/math]. Regardons la soustraction des deux:
[math]1000a+100b+10c+d - (1000d+100c+10b+a)[/math]
[math]=1000(a-d)+100(b-c)+10(c-b)+(d-a)[/math] (On regroupe par puissance de 10)
[math]=1000(a-d)+100(b-c)-10(b-c)-(a-b)[/math] (On inverse le signe des deux derniers)
[math]=(1000-1)(a-d)+(100-10)(b-c)[/math] (On factorise)
[math]=999(a-d)+990(b-c)[/math]
[math]=9 \times (111(a-d)+110(b-c))[/math] (On factorise par 9)
[math]=9x[/math]
Voilà, on vient de prouver que soustraire un nombre avec le même nombre mais les chiffres inversés revient obligatoirement à un multiple de 9. Après, par la propriété des multiples de 9, on retombe sur ce qu'on a vu plus haut. Nonobstant, je rappelle qu'il y a un multiple de 9 particulier sur lequel l'addition successive n'amène pas à 9, c'est le 0. Dans ce cas là, ça amène tout simplement à 0. Est-ce que cela peut arriver dans notre cas? Peut-on avoir une année dont les chiffres inversés donne lui-même? Tout à fait, dans le cas d'années palindromiques. On parle de palindrome lorsqu'un mot ou nombre peut se lire indépendamment de droite à gauche et de gauche à droite. Dans le cas de nos années, 2002 et 1991 sont des palindromes par exemple. Dans ces cas là, il amène à 0 et il suffit d'ajouter dans le liste de Fabien le 0 - Logique pour que le tour marche de partout.
Voilà comment on donne l'illusion du choix et de l'unicité (c'est votre année de naissance, elle vous est propre) et pourtant, on vous amène tous au même résultat. C'est juste la magie des mathématiques.
D'où vient le discriminant et son utilité?
J'imagine qu'on a déjà dû vous apprendre à résoudre une équation du second degré, sinon vous ne chercherez pas un article sur le discriminant en mathématique. On a dû vous expliquer que lorsqu'on avait un polynôme du second degré, du type [math]ax^2+bx+c[/math] et que vous recherchez les racines, c'est-à-dire lorsque ce polynôme s'annule, on cherche un delta majuscule qu'on appelle Discriminant tel que [math]\Delta = b^2 - 4ac[/math] et on regarde son signe. Alors, on gobe ça, ça marche très bien mais on ne nous explique pas toujours d'où il vient. Pourquoi cette valeur [math]b^2 - 4ac[/math] ? Cela sort d'où? Et en quoi son signe nous permet de déterminer les racines d'un polynôme?
Je ne sais pas vous mais personnellement, je n'aime pas apprendre bêtement des choses. J'ai besoin de comprendre. Une fois que j'ai assimilé la logique, je retiens beaucoup plus facilement que du par-cœur car du coup, ça fait sens. Bien sûr, ce n'est pas un savoir caché et certains professeurs l'expliquent et c'est génial. Mais avec la pression du programme et le peu de temps qu'on a pour le faire, certains ont tendance à aller à l'essentiel en donnant les outils sans mentionner pourquoi ils marchent. En réalité, il nous appartient à nous de chercher et une simple recherche sur le net vous amènera la réponse. C'est peut-être même ça qui vous a amené. Donc rentrons dans le vif du sujet.
Pour vous montrer que c'est absolu, générique, je ne vais pas prendre un exemple spécifique et je vais rester avec la fonction [math]f(x) = ax^2+bx+c[/math]. L'idée va être de réécrire cette fonction sous une autre forme. Cette nouvelle forme s'appelle la forme canonique. Tout d'abord, on va factoriser a : [math]ax^2+bx+c = a(x^2+ \frac{b}{a}x + \frac{c}{a})[/math]. Jusque là, ça ne casse pas trois pattes à un canard. Ensuite, c'est là que se passe toute l'intelligence du processus. On note qu'on a presque une identité remarquable. Effectivement, [math](x + \frac{b}{2a})^2 = x^2 + \frac{b}{a}x + (\frac{b}{2a})^2[/math]. On y est presque dans notre cas. Il nous manque juste [math](\frac{b}{2a})^2[/math]. Dans notre polynôme factorisé, on peut ajouter 0 sans rien changer du résultat, vous êtes d'accord? [math]a(x^2+ \frac{b}{a}x + \frac{c}{a}) = a(x^2+ \frac{b}{a}x + 0 + \frac{c}{a})[/math]. Mais pourquoi écrire bêtement 0 lorsqu'on peut écrire [math](\frac{b}{2a})^2 - (\frac{b}{2a})^2[/math]  ? Notre fonction devient [math]f(x) = a(x^2+ \frac{b}{a}x + (\frac{b}{2a})^2 - (\frac{b}{2a})^2 + \frac{c}{a})[/math]. On s'est embêté à retrouver une identité remarquable donc utilisons la : [math]f(x) = a((x +\frac{b}{2a})^2 - (\frac{b}{2a})^2 + \frac{c}{a})[/math]. Bien, on a un carré, l'avantage est qu'on sait que ça sera toujours positif ou nul.
? Notre fonction devient [math]f(x) = a(x^2+ \frac{b}{a}x + (\frac{b}{2a})^2 - (\frac{b}{2a})^2 + \frac{c}{a})[/math]. On s'est embêté à retrouver une identité remarquable donc utilisons la : [math]f(x) = a((x +\frac{b}{2a})^2 - (\frac{b}{2a})^2 + \frac{c}{a})[/math]. Bien, on a un carré, l'avantage est qu'on sait que ça sera toujours positif ou nul.
Maintenant, intéressons-nous à ce qu'il reste. On va notamment les mettre sous le même dénominateur : [math] - (\frac{b}{2a})^2 + \frac{c}{a} = -\frac{b^2}{4a^2} + \frac{c}{a} = \frac{-b^2}{4a^2} + \frac{4ac}{4a^2} = \frac{-b^2 + 4ac}{4a^2} = - \frac{b^2 - 4ac}{4a^2}[/math]. Remettons cela dans notre fonction, on finit avec : [math]f(x) = a((x +\frac{b}{2a})^2 - \frac{b^2 - 4ac}{4a^2})[/math].
Je rappelle le but initial, c'est de trouver pour quel x, on a [math]f(x) = 0[/math]. Donc [math]f(x) = 0 \Rightarrow a((x +\frac{b}{2a})^2 - \frac{b^2 - 4ac}{4a^2}) = 0 \Rightarrow (x +\frac{b}{2a})^2 - \frac{b^2 - 4ac}{4a^2} = 0\Rightarrow (x +\frac{b}{2a})^2 = \frac{b^2 - 4ac}{4a^2}[/math]. On arrive donc à un carré qui doit être égal à un nombre de signe variable. Mais de quoi dépend réellement le signe de ce nombre? De [math]4a^2[/math]? Évidemment que non car a au carré sera toujours positif donc [math]4a^2[/math] aussi. La seule chose qui va faire influer le résultat est le signe de [math]b^2 - 4ac[/math]. Et comme on a la flemme de réécrire ça à chaque fois, on a dit qu'on allait créer une variable pour ça, et on a établi que [math]\Delta = b^2 - 4ac[/math].
Force est de constater qu'on retrouve ici notre discriminant et qu'au final, tout dépend de lui pour trouver l'égalité qui permet de déterminer les x tel que f(x) = 0. Pour être plus précis, tout dépend du signe du discriminant donc travaillons par disjonction des cas.
Si [math]\Delta > 0[/math]
Un carré est égal à un nombre positif. Cela signifie qu'on peut appliquer de part et d'autres de l'équation la fonction racine carrée définie sur [math][0;+\infty[[/math]. On a donc [math](x +\frac{b}{2a})^2 = \frac{\Delta}{4a^2}[/math] [math]\Rightarrow x +\frac{b}{2a} = \sqrt{\frac{\Delta}{4a^2}}\Rightarrow x +\frac{b}{2a} = |\frac{\sqrt{\Delta}}{2a}|[/math].
Ainsi, on arrive à deux cas: [math]x +\frac{b}{2a} = \frac{\sqrt{\Delta}}{2a}\Rightarrow x = \frac{-b+\sqrt{\Delta}}{2a}[/math] et [math]x +\frac{b}{2a} = - \frac{\sqrt{\Delta}}{2a}\Rightarrow x = \frac{-b-\sqrt{\Delta}}{2a}[/math].
Si [math]\Delta = 0[/math]
C'est le cas le plus simple car du coup, [math]\frac{\Delta}{4a^2} = 0[/math]. On se retrouve ainsi avec [math](x +\frac{b}{2a})^2 = 0 \Rightarrow x +\frac{b}{2a} = 0 \Rightarrow x = -\frac{b}{2a}[/math].
Si [math]\Delta < 0[/math]
Dans les réels, un carré ne peut pas égaler un nombre négatif. On s'arrête donc là, il n'y a pas de solution. Point.
Après, ça, c'est dans les réels. Mais pourquoi se borner à cela? On pose [math] -1 = i^2[/math] et nous voici dans les complexes. Or [math]\Delta < 0 \Rightarrow -1 \times \Delta > 0 \Rightarrow i^2 \times \Delta > 0 [/math].
En réécrivant notre delta avec i au carré, on se retrouve donc avec un nombre positif. On n'a donc plus qu'à appliquer le raisonnement vu avec delta positif et on tombe sur : [math]x +\frac{b}{2a} = \frac{\sqrt{\Delta i^2}}{2a}\Rightarrow x = \frac{-b+\sqrt{\Delta}i}{2a}[/math] et [math]x +\frac{b}{2a} = - \frac{\sqrt{\Delta i^2}}{2a}\Rightarrow x = \frac{-b-\sqrt{\Delta}i}{2a}[/math].
Voilà, maintenant, le discriminant n'a plus de secrets pour vous. Vous savez d'où il vient et pourquoi son signe vous donne tant d'informations pour déterminer les racines.
1-1+1-1+1-1+... = 1/2
VSauce a sorti récemment une vidéo que je vois relativement circuler sur l’infini et le fait qu’on puisse compter au-delà de celui-ci. Beaucoup de gens ont du mal à assigner le concept de l’infinité et c’est tout à fait normal. En effet, l’infini distord de nombreuses règles qui amène parfois à des résultats… surprenants. Je me suis dit que j’allais aborder l’un d’eux dans cette rubrique math et il y a des chances pour que j’en fasse également une deuxième qui va s’appuyer sur la présentation d’aujourd’hui.
Avez-vous entendu parler du mathématicien italien Luigi Guido Grandi ? Si oui, c’est surement grâce à sa fameuse série éponyme. Nous sommes en 1703 et Grandi fait une grande analyse de la suite [math]S = \sum_{n=0}^{\infty}(-1)^n[/math] . Houlà, vous paniquez, plein de symboles mathématiques, ça a l’air compliqué. Bah en réalité, cela en a juste l’air. En fait, c’est l’addition 1,-1,1,-1,1,-1 infiniment. C’est juste une alternance de 1 et -1 qu’on additionne. Qu’est-ce que cette série a de spécial ?
Posez-vous la question, qu'est-ce que nous donne [math]1-1+1-1+1-1+1-1+…[/math] ? Certains vont dire « bah 0 car tout s’annule ». Effectivement, si on fait [math](1-1)+(1-1)+(1-1)+…[/math], on ne fait qu’ajouter des 0 donc ça parait logique que cela donne zéro, donc S = 0. Mais quid si je réécrivais la somme comme cela [math]1+(-1+1)+(-1+1)+(-1+1)…[/math] ? Ici, j’aurai 1 et que des éléments qui s’annulent…donc S faudrait 1 ? Mais il me semblait qu’on avait dit que S vaut 0. D’aucuns diront que ça dépend comment l’addition s’arrête. Selon si c’est un -1 ou un 1 alors le résultat sera 0 ou 1 mais, c’est tout le principe de l’infini, cela ne s’arrête pas. On ne peut donc pas déterminer. Il y a donc eux plusieurs écoles, celles du 0 et celles du 1 et les mathématiciens se sont disputés un long moment dessus. Et que diriez-vous si je vous disais qu’il y a même une troisième possibilité pour S ? Elle a été très souvent écartée de par le passé et pourtant, elle existe. Regardez :
[math]S = 1-1+1-1+1-1+…\\
\Rightarrow 1-S = 1- (1-1+1-1+1-1+…)\\
\Rightarrow 1 – S = 1-1+1-1+1-1+…. \\
\Rightarrow 1- S = S\\
\Rightarrow 2S = 1\\
\Rightarrow S = \frac{1}{2}[/math]
Cette somme de 1 et de -1 donnerait une fraction ? Fadaise et billevesée. Et pourtant… avec nos outils mathématiques modernes, on trouve même que c’est le résultat le plus probant. Cette série diverge. En effet, si on regarde les résultats des sommes partielles, on a 1,0,1,0,1,0… Donc selon l’étape où l’on est, on a comme résultat soit 1 soit 0. Il n’y a donc pas de limite, on ne converge pas vers une valeur, dans le sens, on ne se rapproche/tend pas vers une valeur. Cela ne veut pas pour autant dire que mathématiquement, cette somme n’a pas de valeur.
Dans le domaine de la sommation infinie, on a un outil bien pratique nommé la sommation de Cesàro. Rien à voir avec Jules César, mais avec Ernesto Cesàro, mathématicien de son état. Celui propose que plutôt que d’étudier les sommes partielles, on devrait travailler sur la convergence des moyennes des sommes partielles.
Donc, on a tout d’abord, 1. Ensuite, on a [math]\frac{(1+0)}{2} = \frac{1}{2}[/math]. Puis [math]\frac{(1+0+1)}{3} = \frac{2}{3}[/math]. Puis [math]\frac{(1+0+1+0)}{4} = \frac{1}{2}[/math]. Puis [math]\frac{(1+0+1+0+1)}{5} = \frac{3}{5}[/math] et ainsi que suite. Que peut-on dire de cette série ? Eh bien, contrairement à la précédente, celle-ci converge. On note que pour tout n paire, on a comme résultat [math]\frac{1}{2}[/math] et pour tout n impaire, on a une fraction du type [math]\frac{1}{2} + \frac{1}{2n}[/math]. Or, quand on tend vers l’infini [math]\frac{1}{2n}[/math] va devenir de plus en plus infime et tend donc à se rapprocher de [math]\frac{1}{2}[/math]. On peut procéder avec les autres méthodes de sommations infinis comme celle d’Abel ou de Borel, on tombe toujours sur [math]\frac{1}{2}[/math]. Et contre tout attente, cela se justifie très bien comme le tout premier calcul que je vous ai montré qui est la démonstration la plus simple.
Le format papier et racine de 2
Vous le savez surement, on utilise traditionnellement des feuilles de papier au format A4, c'est-à-dire, 21 x 29,7 cm. Vous ne vous êtes jamais demandé pourquoi on a choisi cette taille? Après tout, à la découpe, prendre 29,7 cm ne doit pas être des plus aisés. Pourquoi ces 0,7 centimètres? Et puis, pourquoi le format le plus utilisé est A4? Pourquoi ne l'a-t-on pas appelé A0 et on partirait de lui comme format de référence.
Il faut savoir que cela a été normalisé via l'ISO 216 et est donc internationalement utilisé. Ce n'est donc pas irréfléchi ni un choix anodin. En effet, c'est un choix très pratique et non, ce n'est en réalité pas difficile d'avoir à la découpe. Ils ont fait en sorte que lorsqu'on coupe une feuille au format X(n), cela nous donnerait deux feuilles au format X(n+1). Je mets deux A4 à côté et on obtient une A3. Et si je plie une A4 dans la longueur alors j'obtiendrai une A5. La dessus, je pense ne rien vous apprendre.
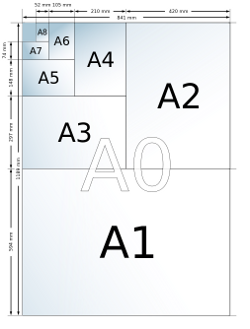
Mais cela ne suffit pas. Car j'ai envie de dire, je coupe par la diagonale et j'obtiens deux triangles qu'il suffit d'ajouter pour constituer le format au dessus. Il fallait garder la même forme rectangulaire et surtout garder les mêmes proportions, c'est-à-dire, que le rapport de la longueur par la largeur devait être égal au celui du format précédent. De cette façon, on aura qu'à appliquer ce rapport sur la taille du dessin ou de la police d'écriture pour le convertir au nouveau format sans que l'oeuvre soit déformée. Il se trouve que cet propriété est rendu possible grâce à racine de deux.
En effet, racine de 2 est le seul nombre à avoir cette propriété là. Pour vous en convaincre, je vous propose de regarder le schémas suivant:
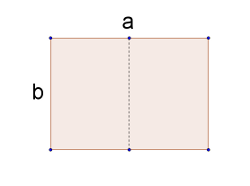
Nous avons un rectangle de longueur a et de longueur b. Et on veut que le rapport des dimensions de ce rectangle soit le même que celui du rectangle obtenu après avoir coupé la feuille en deux sur la longueur et qui a donc comme longueur b et largeur la moitié de a.
En résumé, on veut que :
[math]\frac{a}{b} = \sqrt{2}[/math]
Voilà pourquoi le 0,7 cm est important, pour garder la proportion à racine de 2. Après [math]\frac{297}{210} \neq \sqrt{2}[/math], c'est proche mais ce n'est pas réellement égal. Faut bien penser que cela a été fait en 1922 par la DIN (bureau de normalisation) allemande avant d'être répandu dans le monde et à l'époque, on n'avait pas des outils aussi précis que maintenant.
Alors maintenant, pourquoi A4? Car on est parti du format A0 qui est en fait, le format Aigle inventé et imposé par Napoléon Bonaparte (c'était pour imposer une échelle pour les cadastres de ville) et se voulant être une surface d'un mètre carré. L'erreur vient en réalité de là, car ils ont prit 841 × 1189 mm. Or [math]841 \times 1189 = 999\ 949 \cong 1m^{2}[/math]. Mais globalement, l'erreur est si infime qu'on ne la voit guère.
Pourquoi la somme successive des chiffres d'un multiple de 9 donne 9?
Beaucoup d'énigmes, de tours de magie ou de divination jouent sur cette propriété de prime abord étonnante des multiples de 9. Si je prends n'importe quel nombre non nul et que je le multiplie par 9 alors l'addition successive de ses chiffres nous donnera 9. Par exemple, si je prends [math]541 \times 9 = 4869[/math] or [math]4+8+6+9=27[/math] et [math]2+7=9[/math]. Comme je l'ai susmentionné, cela peut être de prime abord étonnant mais en réalité, celle est tout a fait logique et réside dans le fait qu'en base 10, 9 est le nombre qui précèdent le nombre de la base (en gros [math]9 = 10 -1[/math] et c'est ce qui en fait sa singularité).
Nous travaillons usuellement en base 10, cela signifie que n'importe quel nombre peut être décomposé de tel façon : [math] nombre = ...+d \times 10^{3}+ c \times 10^{2} + b \times 10^{1} + a \times 10^{0} =[/math] [math]...+ d\times 1000 + c \times 100 + b \times 10 + a[/math]. Cela vaut pour tout nombre positif ou nul, sachant que les chiffres a,b,c... peuvent valoir 0. Pour les négatifs, il suffit de rajouter un moins devant. Je vous propose de jouer un peu avec cette écriture: [math]nombre = ...+1000d+100c+10b+a =[/math] [math]....+999d+99c+9b+a+b+c+d+...=[/math] [math]9\times (...+111d+11c+b)+(....d+c+b+a) =[/math] [math]9\times x + (...d+c+b+a)[/math]. Je me suis permis d'ajouter une variable x pour simplifier l'écriture car ce nombre [math](...+111d+11c+b)[/math] ne nous intéresse guère. Ce qu'il faut remarquer, c'est que pour tous nombres en base 10, on peut l'écrire comme un multiple de 9 auquel on ajoute la somme de ses chiffres.
Maintenant, posons que notre nombre de départ soit un multiple de 9, alors [math]9y = 9x + (...+d+c+b+a)[/math]. On a donc un multiple de 9 qui est égal à un multiple de 9 plus une addition de ses chiffres. Pour que cela soit un multiple de 9, alors on a pas le choix, il faut que cette addition de chiffres soit également un multiple de 9. De ce fait, dans le cas où l'on prend un multiple de 9, alors l'addition de ses chiffres nous donnera forcément un autre multiple de 9 plus petit. Cela vaut pour tous multiples de 9. Donc cela vaut également pour le nombre obtenu via l'addition des chiffres d'un multiple de 9 plus grand. On peut donc par récursivité en déduire que les additions successives de multiples de 9 amèneront inévitablement à 9 ou 0 (0 étant un multiple de 9 particulier).
Et...c'est tout. C'est aussi simple que cela. Pas besoin d'avoir fait bac+5 pour comprendre cela, une bonne logique suffit. Mais 9 n'a rien de magique. C'est juste car c'est le nombre précédent la base. Si je travaille en base 8 (en octal) alors les multiples de 7 ont également cette propriété. Par exemple, en base 8, on a [math]7 \times 6523 = 56 505[/math] or [math]5+6+5+0+5 = 25[/math] et [math]2+5 = 7[/math].
Un processus infini peut-il se terminer?
Est-ce qu'un processus infini peut se terminer? Voilà une question forte intéressante. "Stupide" diront certains sans comprendre toute la subtilité scientifique derrière. "C'est trivial" diront d'autres, "par définition, ça n'a pas de fin". La question est en réalité plus subtile que ça car on ne parle pas de fin, on parle de terminer, d'un après, peut-il y avoir un "après" lors d'un processus infini?
Je m'explique. Connaissez-vous le paradoxe de la dichotomie? Il fait parti des fameux paradoxes de Zénon d'Élée, philosophe grec présocratique du Ve siècle avant J.C. Concrètement, il se présente comme sui: Zénon se tient à huit mètres d'un arbre et veut y lancer une pierre. Pour atteindre l'arbre, la pierre va d'abord devoir parcourir la moitié de la distance, soit 4m, puis la moitié des 4m restant, donc 2m, puis ainsi de suite. À chaque itération, il va devoir parcourir la moitié de la distance restante et ce, indéfiniment. Du coup, jamais la pierre ne touchera l'arbre car c'est un processus infini. C'est absurde, je pense que vous pourrez tous attester que la pierre touchera l'arbre (si tant est que Zénon vise bien). Pourtant, si je suis mon raisonnement, jamais il n'est censé le toucher car il restera toujours à la pierre à parcourir l'autre moitié de la distance restante. Que dire alors?
"Simple! Tu ne m'auras pas, Yann. On parle ici du monde réel! Or le monde réel est bornée par la physique. Or la physique nous dit qu'il y a, à un certain niveau, un élément insécable, qu'on ne pourra plus diviser en deux. Pendant longtemps, ce fut l'atome en tant que tel puis avec nos avancées modernes, c'est le quantas qu'on ne peut réduire. Basée sur la constante de Planck, utilisée pour décrire la taille des quantas, la longueur de Planck est une distance qu'on ne peut, à ce jour, physiquement pas réduire. Celle-ci est de [math]l_p = 1.616252 \times 10^{-35}m[/math]. On ne peut alors pas dans le monde réel diviser par deux la distance entre la pierre et de l'arbre indéfiniment! Donc ça ne marche pas car ce n'est pas un processus infini."
 Bah Billie, tu as pris des cours depuis notre dernière rencontre? Bah tu sais quoi? Ce que tu dis est vrai. On ne peut pas physiquement diviser continuellement par deux, on est borné par la constante de Planck et ce qui en découle. En outre, même si on remettait en cause cette constante et trouverait un élément encore plus petit, on ne ferait que réduire cette valeur mais elle ne sera jamais infini. Cependant, on est d'accord que quand le monde abstrait des maths, on peut. Représentons mathématiquement le cheminement de la pierre. On est d'accord qu'à chaque étape, je vais devoir ajouter à la distance précédente un demi de elle-même, ce qu'en terme de suite, on dirait [math]u_{n+1} = \frac{1}{2}u_n[/math]. Et on va faire la somme des éléments de cette suite. Appelons cette somme S et la distance à traverser d. On a donc :
Bah Billie, tu as pris des cours depuis notre dernière rencontre? Bah tu sais quoi? Ce que tu dis est vrai. On ne peut pas physiquement diviser continuellement par deux, on est borné par la constante de Planck et ce qui en découle. En outre, même si on remettait en cause cette constante et trouverait un élément encore plus petit, on ne ferait que réduire cette valeur mais elle ne sera jamais infini. Cependant, on est d'accord que quand le monde abstrait des maths, on peut. Représentons mathématiquement le cheminement de la pierre. On est d'accord qu'à chaque étape, je vais devoir ajouter à la distance précédente un demi de elle-même, ce qu'en terme de suite, on dirait [math]u_{n+1} = \frac{1}{2}u_n[/math]. Et on va faire la somme des éléments de cette suite. Appelons cette somme S et la distance à traverser d. On a donc :
[math]S = \frac{1}{2}d + \frac{1}{4}d + \frac{1}{8}d + \frac{1}{16}d + ...[/math]
Multiplions S par 1/2 :
[math]\frac{1}{2}S = \frac{1}{4}d + \frac{1}{8}d + \frac{1}{16}d + ...[/math]
Et si je soustrais les deux équations, que se passerait-il? Tous les éléments qui continuent à l'infini s'annuleront sauf le premier. On obtiendra :
[math]\frac{1}{2}S = \frac{1}{2}d \Rightarrow S = d[/math]
La distance sera donc atteinte...même dans le monde des mathématiques sans constante de Planck. Car oui, Billie, une somme infinie peut arriver à un résultat fixe et déterminé. L'un des exemples les plus parlant est le suivant:
[math]S = 0.9999...\\
10S = 9.9999...\\
10S = 9 + 0.9999...\\
10S = 9 + S\\
9S = 9\\
S = 1\\
1 = 0.9999...[/math]
Ceci n'est valable que pour l'infini. Il ne peut pas y avoir de dernier 9 sans quoi ça ne serait plus égal mais à l'infini, c'est réellement égal. 1 = 0.9999.... Tout comme [math]d = \frac{1}{2}d + \frac{1}{4}d + \frac{1}{8}d + \frac{1}{16}d + ...[/math]
"Une addition infini qui se traduit par un nombre défini... Je ne sais quoi dire. Tu es sûr qu'il n'y a pas erreur? Que ce n'est pas un raisonnement par l'absurde par exemple". Ok, je vais prendre un autre exemple. On va parler des supertask et de la lampe de Thomson. J'allume une lampe puis j'attends une minute. J'éteins alors la lampe et j'attends moitié moins de temps donc 30 secondes. Je rallume ma lampe et j'attends 15 secondes et je continue le processus d'allumer et d'éteindre la lampe indéfiniment. Comme je divise le temps d'exécution par deux à chaque fois, on est d'accord que comme pour le paradoxe de Zénon, on a ici un processus infini. Or, pour ce processus infini, je réduis le temps de chaque étape de moitié ce qui fait que ce processus infini va durer un instant fini. Au passage, c'est ça qu'on appelle une supertask. Car in fine, qu'y a-t-il à 2 minutes? La lampe est-elle allumée ou éteinte? Car l'infinité des actions s'est déroulée dans ces deux minutes si vous regardez bien. La somme ne va pas nous aider cette fois car elle diverge entre deux états (allumé 1 et éteint -1) qui n'est pas sans rappeler cet article où l'on trouve que la réponse est 1/2 donc que ça peut être soit l'un, soit l'autre. On ne peut le déterminer.
Paul Benacerraf vient alors à notre aide dans son écrit "Tasks, super-tasks, and the modern eleatics". Il souligne que nous sommes incapable de déterminer l'état de la lampe car nos informations ne sont pas complètes. On a mélangé le monde réel (la lampe) et le monde mathématique. Comment fait-on pour que la lampe alterne d'état? Si par exemple, c'est une boule électrique rebondissant sur une plaque conductrice dont la hauteur diminue à chaque fois de moitié comme sur le dessin ci-dessous, alors là, on est capable de déterminer :
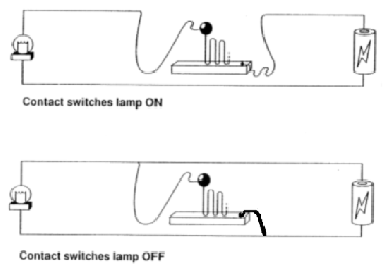
Car on connaît ici la situation finale, la boule cessera de rebondir à la fin de notre supertask et cela nous permet de déduire la situation finale de la lampe en fonction du circuit électrique utilisé. Le fait de mathématiquement pas pouvoir déterminer la situation finale est justement du à cette abstraction du monde mathématique, voilà tout. Il n'en reste pas moins qu'il est totalement possible pour un processus infini de se terminer.
Comment couper N parts égales d'un gâteau
Mardi, c'est l'Épiphanie, cette fête où on tire les rois. Ce fameux jour où on se met tous autour d'une galette espérant tirer la fève pour être le roi de la soirée. Oui mais voilà, si le vieil oncle Bertrand prend une immense part, les autres sont désavantagés. Il en va de l'équité de tous de découper des parts égales. Or selon le nombre d'invités, ce n'est pas toujours des plus faciles. Alors comment couper N parts égales dans un gâteau, une galette et autres ronds?
En fait, il suffit d'appliquer un algorithme itératif très simple. Mais pour l'appliquer, il faut faire un petit calcul. Un rond, je ne vous apprends rien, fait 360°. Donc si on souhaite que toute le monde ait la même part, il faut que chacun ait un angle de [math]\frac{360}{N}[/math]. Prenons l'exemple suivant, on veut 9 parts. Il faudra donc que chaque part ait un angle de [math]\frac{360}{9} = 40°[/math] . Mais vient la grande question, comment prendre intuitivement 40°? Je vous propose de garder cette exemple, et de regarder le schémas ci-dessous:
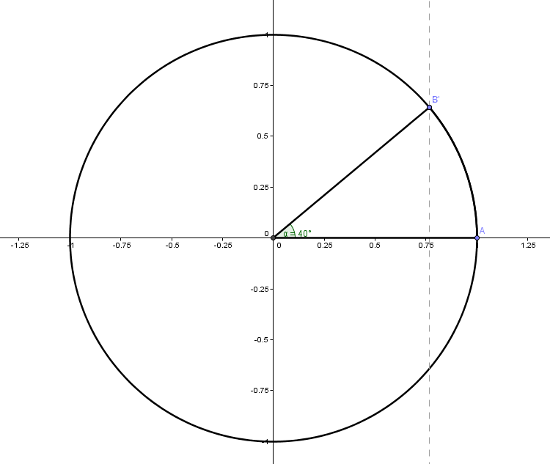
Imaginons, on a commencé par couper du centre O jusqu'au point A. On a donc un rayon de notre cercle. On va savoir où placer notre point B pour être sûr d'avoir un angle à 40°. Regardons où se croise la perpendiculaire à OA passant par B et le segment OA. La perpendiculaire a été représenté en tiret. On note qu'elle se coupe très près du 0.75. Or qu'est-ce que le 0.75? C'est les trois quarts de notre rayon et on sait très simplement calculer ça. On prend la moitié de notre rayon puis la moitié du segment supérieur. Donc, on fait ça, on remonte légèrement plus et après, on prend la perpendiculaire et on regarde sur quel bord de la tarte/galette/gâteau j’atterris. Je n'ai plus qu'à découper du centre à ce bord, ici découper OB.
Ok mais après? Bah A, je l'ai pris totalement arbitrairement. J'ai pris un rayon quelconque et je me suis débrouillé pour en avoir un autre. Imaginons que je prend comme rayon OB, serais-je capable d'appliquer la même méthode pour trouver une autre part? Oui en effet. Il me suffit de reprendre un petit peu plus de 75% de OB et partir perpendiculairement jusqu'à bord de mon cercle et là, j'ai une nouvelle part encore. Et je continue ainsi jusqu'à la fin de mon gâteau. Et comme on est parti de 360°, normalement, il ne devrait pas y avoir de résidu en plus. Exemple avec cette galette qui nous vient de "Le sot l'y laisse" :

Alors vous allez me dire "ok mais si je ne souhaite pas neuf parts mais 6?". Eh bien la logique est exactement la même. La seule donnée qui vous manque est le pourcentage du rayon à prendre. Comme on veut 6 parts, on veut des parts avec des angles de 60°. Plutôt que de regarder à la louche un schémas, pour obtenir ce fameux pourcentage, on doit juste fait en réalité [math]cos(60°) \times 100[/math]. En général, [math]cos(\frac{360}{N}) \times 100[/math] avec N, le nombre de parts souhaité. Il se trouve que pour 6 parts, [math]cos(60°) = 0.5[/math] donc on doit juste prendre la moitié de notre rayon. J'imagine que vous n'avez pas toujours une calculette dans la main quand vous coupez un gâteau donc voici ce qu'il faut se souvenir:
Nb de parts | Angle de la part | Cosinus | % du rayon |
5 | 72° | 0,309 | 30% |
6 | 60° | 0.5 | 50% |
7 | 52° | 0,616 | 60% |
8 | 45° | 0,707 | 70% |
9 | 40° | 0,766 | 75% |
10 | 36° | 0,809 | 80% |
11 | 33° | 0,839 | 85% |
13 | 28° | 0,882 | 90% |
PS: Si vous êtes 13, pensez plutôt à prendre une autre galette car on mange peu avec un treizième du gâteau.
- 1
- 2


