08 Jun
2017
 Par Yann Bidon
Par Yann Bidon
La rupture diplomatique visée contre le Qatar
La rupture des relations diplomatiques entre l’Arabie Saoudite et ses alliés tel que les Émirats Arabes Unis et l’Égypte d’un côté et le Qatar de l’autre a fait pas mal couler d’encre et a engendré pas mal de réactions à droite et à gauche. Je me devais donc d’apporter également ma modeste contribution au débat et c’est ce que je vais tenter de faire via cet article. Je vais tenter de réagir aux commentaires générales et réactions usuelles face à cette annonce et j’espère que vous saurez y voir un peu plus clair dans toute cette histoire.
Mais ce ne sont pas tous des pays musulmans ?
Ma réponse la plus spontanée serait « et alors ? ». Vous savez, en Europe, on était tous chrétiens. Et je vous assure que si vous lisez l’Histoire européenne, ça n’a absolument pas empêché de nous mettre sur la gueule plus d’une fois. Bien que la religion ne puisse pas être invoqué comme casus belli, il est toujours dans l’objectif d’une nation de défendre ses intérêts et étendre son influence (et pourquoi pas son territoire). En l’occurrence, le fait que les pays du Moyen-Orient aient une forte population et un pouvoir proche de la religion musulmane ne les empêchent en rien d’avoir des conflits entre eux. C’est un argument plutôt à côté de la plaque.
D’autant plus qu’à l’instar de la chrétienté, l’Islam est pluriel. On a des catholiques, des protestants, des orthodoxes, des anglicans, des mormons, des témoins de Jehova… tous sont chrétiens et partagent une histoire et une croyance commune mais ça diffère sur certaines manières de faire, sur certains textes à suivre ou interprétations de ces derniers, à quelle institution ou Église se vouer… Certains courants sont plus intégristes que d’autres. Et surtout, ça a été une cause supplémentaire de massacres intrinsèques. Eh bien, figurez-vous que l’Islam est semblable. Elle n’est pas unique et il y a plusieurs courants dont les principaux sont le chiisme, le sunnisme et le kharidjisme. Sachant qu’eux-mêmes ont des sous-mouvements comme le wahhabisme dont l’Arabie Saoudite en est le chantre international. Donc franchement, dire qu’ils ont la même religion, ça ne veut rien dire.
Soit mais ils sont tous deux sunnites, non ?
Oui mais encore une fois, on s’en moque de ça, même si c’est plus cultivé comme question. Faut plus voir ça comme un Game of Thrones (ça vous parle plus ça). Faut regarder les influences, la politique et la stratégie des États.
Pendant très longtemps et avec l’aval des américains et des européens, ce fut l’Arabie Saoudite qui gérait la région. Les grandes réunions et meetings sur le monde oriental ne se faisait pas sans eux, ils se sont posés comme porte-parole du monde arabe. Sauf que depuis sa création en 1932, de nombreuses nations ont percé comme en 1971, lorsque les anglais se sont retirés de la région et les émirats sous protectorat britannique ont repris leur propre gestion, certains se sont rassemblés, formant les Émirats Arabes Unis et d’autres ont refusé de rejoindre cette union et en ont profité pour déclarer leur indépendance comme le Qatar et le Bahreïn. Depuis, les deux premiers ont bien monté, surtout grâce aux ressources naturelles formidables dont leurs terres regorgent. Je pense notamment au gaz pour le Qatar. L’influence du Qatar est grandissante à l’échelle de ses investissements dans le monde entier et notamment en France où Nicolas Sarkozy leur a donné un avantage fiscal pour les attirer. Autre point majeur d’influence, Al Jazeera, une chaine de télévision diffusée à l’international et prend de la place, devenant même le diffuseur d’une coupe de monde de foot. L’Arabie Saoudite n’aime pas qu’on menace son leadership sur la région.
Outre ses achats mirobolants, la Qatar a tissé des liens avec de nombreux mouvements islamistes comme le Hamas très actif sur la bande de Gazas ou encore les frères musulmans, une grosse organisation transnationale dont le printemps arabe lui a été hautement profitable car ayant pu prendre le contrôle sur bon nombre de pays à cette occasion. Et l’Arabie Saoudite n’aime pas du tout les frères musulmans.
Car faut pas croire, la position de l’Arabie Saoudite est aussi contestée dans le monde musulman et même dans le pays. Les Saoud doivent leur pouvoir grâce aux extrémistes religieux du wahhabisme. Donc forcément, la situation religieuse est assez fondamentaliste, ce qui chagrine les musulmans progressistes. Mais dans le même temps, les radicaux reprochent les relations du pays avec les occidentaux et notamment avec l’ennemi tout désigné, les États-Unis d’Amérique. Les US et encore récemment avec le discours de Trump ont rappelé les pays à leurs responsabilités et invité notamment l’Arabie Saoudite à durcir ses actes pour lutter contre la dérive terroriste dont la région semble être le terreau. Une petite tapette sur les doigts qui froissent l’orgueil des dirigeants de l’Arabie Saoudite, une petite accusation de ne pas être à la hauteur.
Donc au final, pas de guerre religieuse, juste un problème d’égo ?
Déjà, ne nous emballons pas, ce n’est pas une guerre. C’est une rupture diplomatique. C’est plus un avertissement et un rappel à l’ordre. On n’est pas encore à la guerre. Mais plus qu’un problème égo, c’est vraiment un jeu de pouvoir pour la région. Et…je n’ai pas encore tout dit et effectivement, la religion a un peu sa part de responsabilité mais pas avec le Qatar…Avec l’Iran.
L’Iran est un très grand pays (en termes de superficie) et dispose également de ressources naturelles importantes et qui font sa fortune. Contrairement à ses voisins, ce dernier est chiite, progressiste et tient des élections plus démocratiques qui ont d’ailleurs donné vainqueur un progressiste en la personne de Rohani. Comme si ça ne suffisait pas, il soutient le régime de Bachar Al-Assad honni en Europe et aux USA et soutient militairement les rebelles du Yémen contre une coalition menée par nul autre que l’Arabie Saoudite depuis 2014 (et la guerre civile dure toujours mais ça, on n’en parle pas, faut mieux parler des ruptures diplomatiques, les symboles valent mieux que la vie des enfants massacrés là-bas).
Inutile de vous dire que dans la région, l’Iran, c’est le diable. D’ailleurs lors de son discours, Trump a clairement ciblé l’Iran comme l’ennemi, appuyant encore la haine value par l’Arabie. Mais tout le monde n’est pas aussi radical qu’eux. Oman, le Koweït et le Qatar travaillent volontiers avec l’Iran faisant fi des distorsions religieuses et du haro mis par les Saoudiens. Alors Oman et le Koweït sont plus docile et reste dans le giron saoudien. Le Qatar lui est plus indépendant et insoumis.
Cette mise au ban par les pays de la région ambitionne de remettre le Qatar dans le rang et de réorienter sa politique notamment étrangère sur l’Iran et lui rappeler que c’est eux les patrons, c’est eux les gendarmes de la région et que maintenant, ça suffit. C’est un coup de force dans un bras de fer de contrôle de la région et d’influence mondiale. L’Arabie Saoudite veut se réaffirme et se remettre sur le devant de la scène en montrant qu’elle gère les choses, elle recadre les pays dissidents et continuent la guerre froide avec l’Iran, conformément à la volonté américaine. Après, c’est compliqué pour la Qatar car ils partagent avec l’Iran leur immense puits gazier.
Et genre, ils n’ont rien trouvé comme raison que « Le Qatar soutient des organisations terroristes ». Ils ne sont pas un peu hypocrites sur les bords ?
Tout à fait. L’Arabie Saoudite est loin d’être une image de Sainteté. Je rappelle mon article sur le projet afghan et la création d’Al-Qaïda. Elle est soupçonnée de financer bien des mouvements armés de manière indirecte et discrète. Ainsi leur voir exposer ses torts au Qatar m’a fait bien rire. Mais c’est de la politique. Ils ne vont pas dire qu’ils ont financé et armé (ou aidé à armer) des organisations terroristes causant des milliers de morts, vous pensez bien. Il parait que ça fait mauvais genre au diner des nations.
Et donc que va-t-il se passer maintenant ?
Je ne suis pas Madame Irma moi ! Je me souviens de Fouquet qui, à faire trop bling bling et m’as-tu vu à vexer des Hommes puissants et ça a causé sa chute. Peut-être est-ce ce qui va arriver avec le Qatar (mais j’en doute). Vont-ils se plier? C’est compliqué, c’est un gros aveu de faiblesse et actuellement, ils sont plus dans la posture de l’atteinte à la souveraineté. Les tensions montant ainsi, va-t-on partir faire une dégradation voire une explosion du monde arabe ? Il ne faut peut-être pas abuser. L’Iran et l’Arabie Saoudite ne s’entendent pas du tout, du tout et pourtant, il n’y a pas de guerre frontale entre les deux car ils sont suffisamment intelligents pour savoir que ça serait bon pour personne. Donc avec un pays comme le Qatar où ils ont plus d’accointance, je ne pense pas. Je vois personnellement plus ça comme une tentative de l’Arabie Saoudite à se repositionner comme le gendarme de la région et remettre ainsi les brebis égarées dans le droit chemin. Après les cartes sont dans les mains du Qatar. Va-t-il se plier ou affirmer sa souveraineté et à quel prix ? Bah c’est à lui de moi, pas à moi, cessez de m’importuner ! Moi, je dis des faits pour expliquer les causes, pas des prédictions.
10 Apr
2017
 Par Yann Bidon
Par Yann Bidon
Il faut surmonter dialectiquement nos altérités réciproques
Mais qu’est-ce donc que ce titre alambiqué ? C’est une citation d’Hegel, un philosophe allemand, que Acadomia avait repris lors d’une campagne de pub. Vous avez sans doute pu la voir dans un métro ou bus. La volonté de la pub était volontairement d’être pédant pour que vous n’y comprenez rien et qu’on vous fasse comprendre que vous avez besoin de cours. Je vous propose néanmoins, et gratuitement, de disséquer un peu cette phrase. Commençons par l’altérité. On reconnait ici le préfixe alter- comme dans alter-égo, altermondialiste…, on peut donc en conclure que ça a un lien avec « autre ». Et vous auriez raison, l’altérité est un concept philosophique désignant tout ce qui est autre, ce qui n’est pas dans notre vision des choses, dans notre vision du monde, ce qu’on appelle plus communément notre paradigme. Les altérités, c’est donc tout ce qui sort du cadre, qui ne va pas dans notre sens. Pour vulgariser, je peux dire que c’est tout ce qui nous est différent. Donc lorsqu’on parle d’altérités réciproques, on veut dire que chacun de nous à une vision différente des choses et on va aboutir à des avis, valeurs, positions divergentes. Et c’est cette divergence d’opinions qu’il va falloir surmonter mais pas n’importe comment, dialectiquement. La dialectique est une pratique philosophique très prisée durant la Grèce Antique. C’est l’art de dialoguer avec des personnes d’avis opposés afin justement d’affiner sa propre pensée et en tirer le meilleur de cette confrontation d’idées. Cela rejoint le triptyque « thèse – antithèse – synthèse ». On a notre propre position, c’est notre thèse. On va alors débattre avec une personne avec un avis différent et va donc nous fournir l’antithèse. De là, il va falloir en tirer le meilleur pour pouvoir s’élever et avec une opinion plus précise, améliorée. C'est d'ailleurs cette dernière phase qui la distingue du débat, le but n'est pas à tout prix de convaincre l'autre mais de tirer des enseignements de ce dernier pour affiner sa propre position. C’est en confrontant deux visions différentes qu’on voit la tangibilité de nos choix et ce qu’il faut creuser au besoin. Cela permet également de soulever des points auxquels on n’aurait pas pensé autrement. Ce n’est pas qu’on est bête mais simplement qu’on a, justement, une expérience et un paradigme différents, ainsi, on ne pense pas toujours à tout. Cette phrase d'Hegel traduit donc la nécessité de surmonter nos différences pour en tirer le meilleur et, en conclusion, grandir.
Pourquoi je parle de ça? Récemment, j'ai posté sur mon Facebook politique une message faisant suite au second débat présidentiel et sur un certain candidat notamment. Des gens du bord opposé au mien ont alors exprimé leur désaccord. J'ai alors tenté d'expliquer mon raisonnement et ma pensée plus en détail. Mais je peux généraliser sur l'entièreté de ma page où, in fine, j'ai surtout des commentaires contestataires. Des amis plus proches de mes idées me demandent alors pourquoi je conserve ces personnes? Pourquoi je m'évertue encore et toujours à leur répondre alors qu'ils ne changeront pas? Pourquoi ne les virais-je pas de ma page pour pouvoir être en paix? La réponse réside dans cette citation de Hegel. C'est par l'apport de l'autre et surtout de ceux qui nous sont opposés que l'on grandit. C'est très bien de se sentir soutenu mais globalement, ça n'apporte rien. D'ailleurs, la plupart de ces personnes se contentent de mettre des likes plutôt que de mettre un commentaire avec des arguments complémentaires ou rebondir sur une chose qu'on a dite. Alors que les contestataires, eux, ce sont les premiers à réagir avec plus ou moins de véhémence. Ils vous challengent. Ils décident de confronter votre pensées par la leur. Cela se trouve, ils vont me prouver, par la solidité de leurs arguments et la cohérence de leur raisonnement, que j'ai tort sur un point. Ils auront alors "gagné" et réussi à me convaincre. Mais je n'ai pas perdu la bataille, il n'y a pas de perdant si on est capable de faire de la dialectique. Je me suis enrichi de cette discussion. Elle m'a apporté un complément. Alors bien sûr, sur le moment, ça peut faire mal. On se dit "ha il est chiant avec ses théories communistes/frontistes/centristes/gauchistes/droitards". Mais objectivement, c'est surtout eux qui nous pousse le plus à réfléchir, à se positionner davantage, à remettre en perspective ce que l'on croit. C'est en se mettant constamment en question, en nous poussant dans nos retranchements qu'on tend le plus vers l'objectivité.
J'entends beaucoup parler de tolérance, de vivre ensemble de part et d'autres. Je trouve hélas que ces mots ont perdu de leur substance. C'est devenu "supporter leur présence", ils sont là, on ne va pas les emmerder mais on ne se mêle pas plus. On "fait avec". Mais ce n'est pas ça le vivre ensemble, ce n'est pas ça la tolérance. C'est accepter l'autre, c'est s'enrichir de ses différences et l'enrichir également. Lorsqu'on est en entreprise, je me moque bien de la religion de mon collègue. On œuvre ensemble pour réaliser notre travail. Hé bien, ici, c'est pareil. On a des avis différents mais on échange et on s'apporte mutuellement pour atteindre un idéal, pour toucher du doigt la vérité. Car foncièrement, on n'est pas si différent que ça, on cherche tout à vivre dans un monde meilleur où l'on pourrait y être heureux. La manière d'y atteindre est différente mais l'objectif final est le même. Ce n'est donc qu'en surmontant nos altérités réciproques qu'on pourra s'élever.
Alors, ne me faites pas dire ce que je n'ai pas dit. J'adore être avec des personnes de mon bord. Je passe d'excellents moments avec eux et ça, rien ne le remplacera. Ce sont mes amis. Et ils m'apportent aussi énormément quand je discute profondément avec eux. On peut se donner des arguments, des exemples, des idées, parler de notre vécu et de nos expériences. On est là quand ça va mal, on s'entraide, solidaire. Moi, plutôt qu'un like de soutien, quand je vois qu'un ami se fait lyncher à cause d'un de ses propos, je lui montre mon soutien et apporte ma pierre au débat pour montrer les raisons qui l'on amené à dire ça. On explique, on fait de la sensibilisation, on débat. Les réunions politiques servent notamment à ça. La personne explique sa position et ses choix, pourquoi il a fait ça, pourquoi il lutte. En outre, je reste relativement convaincu de mes valeurs et bien qu'ouvert à la discussion, je reste sur un certain noyau dur, un socle de repères qui me sera très difficile de récuser. Mais je ne suis pas dans le rejet de l'autre.
Une chose que je trouve nocif aujourd'hui en politique est la polarisation de celles-ci. Il y a maintenant des chasses gardés. Des positions dites "de droite" et d'autres "de gauche". Je pourrai très bien l'expliquer mais Science4All a déjà fait une excellente vidéo que je vous invite à regarder <youtube>UIQki2ETZhY
On tend alors vers deux camps de plus en plus marqués, divisés et avec une vision de l'autre de plus en plus délétère. On se dirige vers un schisme politique et idéologique de plus en plus important. C'est regrettable sachant qu'on est amené à vivre tous ensemble. C'est en rejetant les gens comme on a tendance à le faire désormais et en vivant "entre soi" comme le pousse les sites comme Google, Facebook, etc, en favorisant des résultats proches de notre vision, qu'on se marginalise, qu'on se radicalise et ce n'est bon pour personne. Donc ami lecteur, vous pourrez continuer à "critiquer" au bon sens du terme (si c'est un reproche stérile, continuez à vous abstenir^^).
12 Mar
2017
 Par Yann Bidon
Par Yann Bidon
Expliquons ce tour de Fabien Olicard
Fabien Olicard est un mentaliste que je suis depuis un moment et j'ai même eu la chance de le voir en spectacle récemment à Lyon. Il a sorti une vidéo dans lequel il essaie de nous bluffer. C'est un tour mathématique donc forcément, l'impact sur moi fut moindre mais il est toutefois assez ludique et peut faire son effet sur les non-initiés. Je vous propose de le découvrir ici et j'expliquerai le tour plus en profondeur juste après:
<youtube>TTf4RP3EnY8
Évidemment, vous n'aviez en réalité pas le choix. Vous ne pouviez tomber que sur "Logique". Pourquoi? Eh bien, c'est logique  . Il a utilisé la propriété des multiples de 9 dont j'ai parlé dans un précédent article. Pour tout multiple de 9 non nul, la somme successive des chiffres qui le compose aboutira inlassablement à 9. Et dans sa grille, si on regarde le positionnement du mot logique, on le trouve à la position 9, 18 et 27 (tous des multiples de 9). Sachant qu'une différence d'année restera dans le pire des cas à 4 chiffres, il avait anticipé que vous ne pourrez aller plus loin.
. Il a utilisé la propriété des multiples de 9 dont j'ai parlé dans un précédent article. Pour tout multiple de 9 non nul, la somme successive des chiffres qui le compose aboutira inlassablement à 9. Et dans sa grille, si on regarde le positionnement du mot logique, on le trouve à la position 9, 18 et 27 (tous des multiples de 9). Sachant qu'une différence d'année restera dans le pire des cas à 4 chiffres, il avait anticipé que vous ne pourrez aller plus loin.
Cependant, d'où sort le nombre 9? Après tout, il vous a demandé de prendre votre année de naissance. C'est propre à chacun. Et c'est vrai. Néanmoins, la manipulation qu'il vous demande de faire aboutira toujours au même résultat, ça donnera un multiple 9. Je m'explique. Prenons un nombre quelconque en base 10 sur 4 chiffres : [math]a \times 1000+b \times 100+c \times 10+d[/math]. Si on inverse l'ordre des chiffres, on obtient alors [math]d \times 1000+c \times 100+b \times 10+a[/math]. Regardons la soustraction des deux:
[math]1000a+100b+10c+d - (1000d+100c+10b+a)[/math]
[math]=1000(a-d)+100(b-c)+10(c-b)+(d-a)[/math] (On regroupe par puissance de 10)
[math]=1000(a-d)+100(b-c)-10(b-c)-(a-b)[/math] (On inverse le signe des deux derniers)
[math]=(1000-1)(a-d)+(100-10)(b-c)[/math] (On factorise)
[math]=999(a-d)+990(b-c)[/math]
[math]=9 \times (111(a-d)+110(b-c))[/math] (On factorise par 9)
[math]=9x[/math]
Voilà, on vient de prouver que soustraire un nombre avec le même nombre mais les chiffres inversés revient obligatoirement à un multiple de 9. Après, par la propriété des multiples de 9, on retombe sur ce qu'on a vu plus haut. Nonobstant, je rappelle qu'il y a un multiple de 9 particulier sur lequel l'addition successive n'amène pas à 9, c'est le 0. Dans ce cas là, ça amène tout simplement à 0. Est-ce que cela peut arriver dans notre cas? Peut-on avoir une année dont les chiffres inversés donne lui-même? Tout à fait, dans le cas d'années palindromiques. On parle de palindrome lorsqu'un mot ou nombre peut se lire indépendamment de droite à gauche et de gauche à droite. Dans le cas de nos années, 2002 et 1991 sont des palindromes par exemple. Dans ces cas là, il amène à 0 et il suffit d'ajouter dans le liste de Fabien le 0 - Logique pour que le tour marche de partout.
Voilà comment on donne l'illusion du choix et de l'unicité (c'est votre année de naissance, elle vous est propre) et pourtant, on vous amène tous au même résultat. C'est juste la magie des mathématiques.
12 Mar
2017
 Par Yann Bidon
Par Yann Bidon
Pourquoi la somme successive des chiffres d'un multiple de 9 donne 9?
Beaucoup d'énigmes, de tours de magie ou de divination jouent sur cette propriété de prime abord étonnante des multiples de 9. Si je prends n'importe quel nombre non nul et que je le multiplie par 9 alors l'addition successive de ses chiffres nous donnera 9. Par exemple, si je prends [math]541 \times 9 = 4869[/math] or [math]4+8+6+9=27[/math] et [math]2+7=9[/math]. Comme je l'ai susmentionné, cela peut être de prime abord étonnant mais en réalité, celle est tout a fait logique et réside dans le fait qu'en base 10, 9 est le nombre qui précèdent le nombre de la base (en gros [math]9 = 10 -1[/math] et c'est ce qui en fait sa singularité).
Nous travaillons usuellement en base 10, cela signifie que n'importe quel nombre peut être décomposé de tel façon : [math] nombre = ...+d \times 10^{3}+ c \times 10^{2} + b \times 10^{1} + a \times 10^{0} =[/math] [math]...+ d\times 1000 + c \times 100 + b \times 10 + a[/math]. Cela vaut pour tout nombre positif ou nul, sachant que les chiffres a,b,c... peuvent valoir 0. Pour les négatifs, il suffit de rajouter un moins devant. Je vous propose de jouer un peu avec cette écriture: [math]nombre = ...+1000d+100c+10b+a =[/math] [math]....+999d+99c+9b+a+b+c+d+...=[/math] [math]9\times (...+111d+11c+b)+(....d+c+b+a) =[/math] [math]9\times x + (...d+c+b+a)[/math]. Je me suis permis d'ajouter une variable x pour simplifier l'écriture car ce nombre [math](...+111d+11c+b)[/math] ne nous intéresse guère. Ce qu'il faut remarquer, c'est que pour tous nombres en base 10, on peut l'écrire comme un multiple de 9 auquel on ajoute la somme de ses chiffres.
Maintenant, posons que notre nombre de départ soit un multiple de 9, alors [math]9y = 9x + (...+d+c+b+a)[/math]. On a donc un multiple de 9 qui est égal à un multiple de 9 plus une addition de ses chiffres. Pour que cela soit un multiple de 9, alors on a pas le choix, il faut que cette addition de chiffres soit également un multiple de 9. De ce fait, dans le cas où l'on prend un multiple de 9, alors l'addition de ses chiffres nous donnera forcément un autre multiple de 9 plus petit. Cela vaut pour tous multiples de 9. Donc cela vaut également pour le nombre obtenu via l'addition des chiffres d'un multiple de 9 plus grand. On peut donc par récursivité en déduire que les additions successives de multiples de 9 amèneront inévitablement à 9 ou 0 (0 étant un multiple de 9 particulier).
Et...c'est tout. C'est aussi simple que cela. Pas besoin d'avoir fait bac+5 pour comprendre cela, une bonne logique suffit. Mais 9 n'a rien de magique. C'est juste car c'est le nombre précédent la base. Si je travaille en base 8 (en octal) alors les multiples de 7 ont également cette propriété. Par exemple, en base 8, on a [math]7 \times 6523 = 56 505[/math] or [math]5+6+5+0+5 = 25[/math] et [math]2+5 = 7[/math].
28 Jan
2017
 Par Yann Bidon
Par Yann Bidon
Les mérovingiens - Les rois de France
Une amie me demanda si je pouvais lui faire un petit condensé sur les rois de France. Évidemment, votre humble serviteur accepta bien volontiers. On commence donc cette petite série sur les rois de France et cela débute bien évidemment par les mérovingiens.
Tout d’abord, commençons par casser le mythe de la Gaule. Non, la Gaule n’était pas unie. Sous l’occupation romaine, c’était des tribus éparses qui commerçaient et combattaient en tant que mercenaires mais ce n’était pas une seule région fédérée. Les romains distinguaient d’ailleurs deux Gaules, en témoigne le livre de César.
Ce n’est que vers 375 que des royaumes apparuent. Pourquoi ? Car les Huns, un peuple nomade d’Asie Centrale, marchaient sur l’Europe de l’Ouest avec le terrible Attila à leur tête. Beaucoup fuirent les affres de la guerre qui s’approche de l’Europe de l’Est. Cela créa un flux migratoire très important. Pour survivre, les pillards ne trouvèrent rien de mieux que d’attaquer les maisons, les villages, piller les récoltes… Ce fut l’époque des invasions barbares. Ces barbares finirent par s'installer en Europe de l'Ouest. Ainsi ils fondèrent de nombreux royaumes. Nous pouvons citer les Wisigoths en Aquitaine (dès 418), les Alamans vers Strasbourg et Metz, les Burgondes (le Lyonnais et le Dauphiné avec une partie de la Suisse). Mais ce qui nous intéresse le plus est le royaume des Francs Rhénans (ceux qui sont le long du Rhin) et le royaume des Francs Saliens au Pays Bas. Eh oui, au départ, il y avait deux royaumes de Francs. Mais notre héritier à nous est le royaume des Francs Saliens (peu cher, on vient donc des Pays-Bas au départ). Bref, le roi de ce royaume est Clodion le Chevelu.
Rome est sur le déclin, surtout depuis la division de l’Empire en deux et les Wisigoths, les Alains et les Burgondes mène la vie dure aux romains sans compter les révoltes paysannes à cause des taxations élevées et des abus de pouvoir. Du coup, entre 432 et 435, le gros de l’armée affronte ces royaumes…et laisse l’actuel Belgique avec bien peu de défenses. Sentant l’opportunité, ni une ni deux, Clodion partit à la conquête de la Belgique. Cela fut plutôt victorieux :
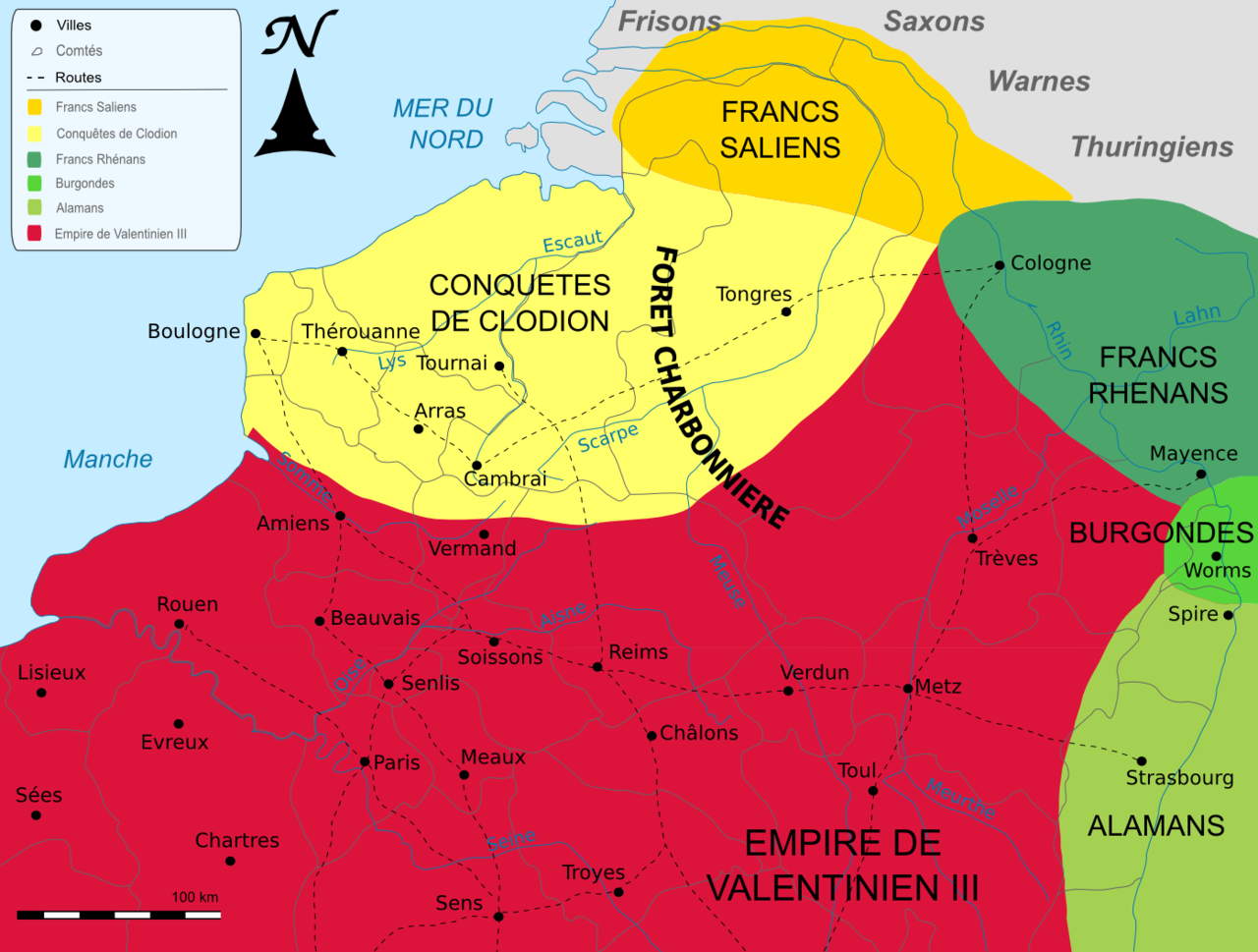
Mais au final, Clodion ne marqua que peu l’Histoire contrairement à son fils, le roi Mérovée.
Les Huns sont aux portes de l’Empire romain et la tension monte. C’est finalement en 451 qu’ils lancèrent leur assaut et envahirent la Gaule Romaine ainsi que tous les royaumes alentours. Mérovée les battit dans la plaine du Santerre. Impressionnée, les romains scellèrent une alliance avec les francs-saliens. Les romains reconnurent le royaume francs-saliens contre leur aide face à Attila. Se déroula alors une bataille sanglante entre Châlons-en-Champagne et Troyes avec les romains du général Aetius et les francs-saliens de Mérovée, toujours en 451. Ils réussirent là où personne encore n’avait réussi, ils mirent en déroute le grand et le puissant Attila et son armée de Huns qui partirent se replier en Europe de l’Est. Cette victoire consolida l’influence et l’importance du royaume des Francs-saliens. Grâce à Mérovée, les francs-saliens avaient enfin un royaume en paix, loin de Rome et de la menace Huns, devenant une grande puissance de la Gaule du Nord. En hommage à ce roi victorieux, la dynastie issue de lui prendra le nom des mérovingiens ! À l’inverse, l’Empire romain en sortit affaibli et perdit beaucoup de sa Gaule Romaine, ils ne leur restèrent que le nord de l’actuel France, dirigé par le général Syagrius.
De Mérovée succéda Childéric Ier. On se moque un peu de lui... C'était un bon petit soldat de Rome avec qui il entretint de bonnes relations. Ils combattirent ensemble notamment contre les Saxons. Mais sans plus. Ce qui est à noter est que c'est sous son règne que Paris commença à se rebeller et partir en guerre civil entre d'un côté les pro Syagrius et les pro-francs. Le plus important est que de Childéric Ier naquit Clovis Ier.
En 481, la France est un petit territoire qui n’a rien à voir avec les frontières d’aujourd’hui en témoigne la carte suivante :
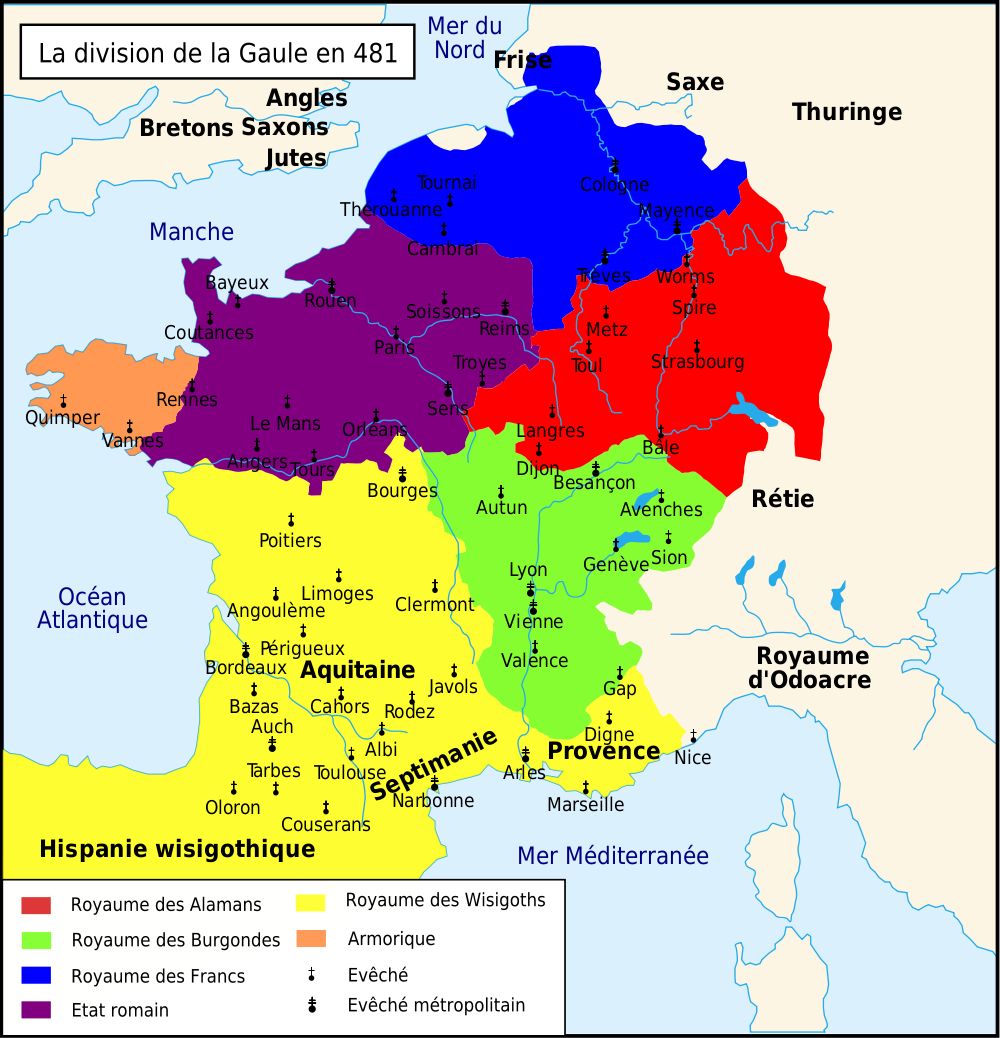
Clovis avait une seule ambition, agrandir le royaume de ses aïeux. Avant 486, il scella un mariage avec la princesse des francs rhénans pour unir le royaume des Francs. Fort de sa position et de son armée, il s’attaqua alors, en 486 (il ne perd pas de temps, le petit), au bout de l’Empire romain restante, celui administré par le général Syagrius. Il eut une grande bataille à Soisson où les deux s’affrontèrent ardemment mais victoire fut donné aux Francs. La province romaine devint franque et Syagrius tenta de trouver refuge chez les Wisigoths qui, pour acheter les faveurs de Clovis, le livrèrent à ce dernier. Ce succès permit à Clovis de contrôler la quasi-totalité de la Gaule du Nord.
L’évêque de Reims, le futur Saint Rémi, incita Clovis à aider les chrétiens de son royaume. Ils devinrent proche. Toutefois, Clovis refusa de se convertir de peur de perdre le soutien de son peuple et de ses guerriers restés païens contrairement aux autres barbares qui se sont très vite christianisés (bien que ariens). Pour l’inciter davantage à se convertir, il arrangea un mariage avec une princesse chrétienne. Ainsi Clovis épousa en 492 en secondes noces la princesse Clotilde du Royaume des Burgondes, scellant par la même un pacte de non-agression entre les deux royaumes. Cette dernière ne cessa d’essayer de convertir son mari.
Clovis continua ses ambitions expansionnistes et s’attaqua en 496 au royaume des Alamans. Malheureusement pour lui, cette bataille ne fut guère glorieuse. Son armée est en déroute et le voilà encerclé et à la merci de l’ennemi. Les barbares dont les francs font partis ne jurent que par la force que les dieux leur donnent. Or les dieux païens ont, semble-t-il, abandonné Clovis. En désespoir de cause, il tenta alors de prier Jésus Christ et jura de se convertir s’il lui apportait la victoire. C’est alors que le chef ennemi tomba sous le coup d’une arme à distance. Leur chef mort, les soldats battirent en retraite. Clovis en profita alors pour renverser la situation. Homme de parole et comptant également obtenir le soutien de l'Église institutionnelle, un des derniers vestiges romains, il tint sa promesse et se fit baptiser à Reims. Ce fut le premier roi franque chrétien.
L’empereur romain d’Orient, Anastase est très inquiet de la puissance des Goths. Il soutint alors Clovis lorsqu’en 507, les Francs attaquent le royaume des Wisigoths. La défaite de la bataille de Vouillé porta un coup dévastateur aux Wisigoths qui durent se replier jusqu’au-delà des Pyrénées, en Espagne. Vainqueur, ce grand chef de guerre fut décoré Consule honoraire par l’empereur romain d’Orient, marquant les bonnes relations entre les deux pays malgré qu’il les ait boutés hors de Gaule. Il contrôla désormais, le Nord et le Sud de la Gaule, seul restait le royaume de Burgondes dont sa femme Clotilde lui assurait le soutien. Il décida de faire de Paris la capitale de son royaume.
Tout se passa bien mais bon, il fallait bien qu’un jour, il meurt en 511. C’est notre lot à tous. Et vient un truc très nul ! La loi de succession de l’époque suivit par les Francs est pourrie. Elle consiste à diviser les terres entre les héritiers mâles. Ainsi, le royaume fut séparé entre les 4 enfants de Clovis. On distingue l’Austrasie (l’ancienne région du Royaume Francs), la Neustrie (l’ancienne province romaine), la Burgondie et l’Aquitaine.
Dernier enfant de Clovis, Clotaire 1er réussit à la mort de ses frères à réunir le royaume mais à sa propre mort, le royaume re-fut divisé entre ses 4 enfants. Et ça continue comme ça pendant un moment. On a eu Clotaire II, petit-fils de Clotaire I, qui réunifia le royaume puis son fils Dagobert 1er fit de même et ainsi de suite encore et encore jusqu’à Childéric III qui se fera déposer par Pépin le Bref.
C’est ainsi que se termine la dynastie mérovingienne. De petites tribus néerlandaises, le royaume Franc sut s’étendre dans toute la Gaule et occuper des frontières qu’on lui connaît mieux. Le royaume Franc réussit à s’affirmer et à profiter du déclin romain pour prendre en charge l’administration de la Gaule du Nord.
16 Apr
2017
 Par Yann Bidon
Par Yann Bidon
Le vote utile
2002, la France se prépare à voter pour la présidentielle d'avril. Après 5 ans de cohabitation, le président sortant, Jacques Chirac, officiellement investi par le RPR, et le premier ministre sortant, Lionel Jospin, officiellement investi par le PS, sont donnés comme favoris. Comme je l'ai déjà expliqué dans un précédent article dénonçant les dérives de notre système électoral, ce dernier favorise le bipartisme. Ainsi, tout le monde s'attend à un duel au sommet entre Jospin et Chirac. La presse se faisait écho du duel de titan à venir et tout deux menèrent une grande campagne. Je me souviens d'un journaliste qui proposait à Jospin différent scénarios et un d'eux était "et si vous n'étiez pas au second tour", ce à quoi Jospin avait répondu qu'il avait beaucoup d'imagination mais que cette dernière a quand même ses limites. Il était persuadé d'être qualifié au moins au second tour.
Et c'est compréhensible, il a le système avec lui. Ce dernier favorise le bipartisme car en votant pour un parti tiers (dont on peut être plus proche) mais qui est plus petit, on pénalise le plus grand candidat proche de nos valeurs et principes. Notre voix, bien qu'importante pour ce petit candidat, est "perdue" dans le sens où elle n'est valable qu'exclusivement pour ce petit candidat qui n'a, en théorie, aucune chance d'être élu. Elle se fait alors au détriment du "grand" candidat le plus près de notre tendance politique et favorise ainsi le camps opposé quel qu'il soit. De là est né le principe de vote utile. On est incité à ne plus voter pour le candidat qui nous est, dans l'absolu, le plus proche mais le grand candidat de la tendance qui nous est la plus proche. Qu'on soit clair, ceci est un fléau anti-démocratique. Je le dénonce mais pour l'heure, le système électoral est ainsi fait. Alors on a le second tour pour reporter nos voix sur les "grands" mais encore faut-il que ces derniers soient qualifiés. Or, contrairement aux législatives où au dessus d'un certain pourcentage, on est qualifié au second tour, donnant ainsi des seconds tours à trois voire quatre candidats, les présidentielles ne prennent que les deux meilleurs, point. Le vote utile est alors encore plus impératif.
Sauf qu'en 2002, les gens n'ont plus voté utile. Cela peut s'expliquer par plusieurs choses (une élection étant toujours complexe). Tout d'abord, la campagne médiatique pro-jospin qui le plaçait en grand vainqueur. En conséquence, certaines personnes se sont dit "je peux me permettre pour une fois de voter pour mes réelles convictions car de toute façon, il sera qualifié, ce n'est pas ma voix qui va changer quoi que ce soit" (sauf que si tout le monde se dit ça...). En outre, Jospin avait un programme assez proche de Chirac et on lui reprochait de ne pas avoir un programme assez socialiste. Ainsi des gens de gauches ont préféré voter pour d'autres candidats plus à gauche. Ainsi, en 2002, les "petits partis" ont eu de bons résultats comme Arlette Laguiller de "Lutte Ouvrière" avec 5.72%, Noël Mamère de "Les verts" avec 5,25 %, Olivier Besancenot de la "Ligue communiste révolutionnaire" avec 4,25 % ou encore Robert Hue du "Parti communiste" avec 3,37 % et pour le lol, Christiane Taubira du "Parti radical de gauche" avec 2,32 %. Sauf qu'à coup de 4/5% par ci par là, ils réduisent le pourcentage restant. La droite relativement unie derrière Chirac eu 19,88 % des voix et l'extrême droite est toujours unie derrière la figure de Jean-Marie Lepen avec 16,86 %. Finalement, avec l'éparpillement des voix de gauche, Lionel Jospin ne remporte que 16,18 %. Et c'est ainsi que le favori fut finalement écarté dès le premier tour de la fonction suprême. Au final, le fait qu'on le déclare favori l'a plus défavorisé qu'autre chose. Et c'est ainsi que le peuple de gauche a dû se résoudre à choisir entre Lepen et Chirac (ou ne pas voter ou voter blanc mais qui sont, à ce jour, sans incidence). Jospin n'a pas su mobiliser derrière sa candidature, il n'a en réalité pas su appeler les gens à voter utile. Alors évidemment, on ne le dit pas, on ne dit pas au gens "voter utile" car ça fait mauvais genre. On préfère diaboliser le camps opposé tel que "voter pour moi ou vous aurez un tel ou un tel après". Mais ne nous leurrons pas, on demande à voter utile. Tout simplement car sans ça, de grands partis peuvent s'écrouler (face à un autre grand parti opposé et jamais en faveur d'un petit parti de notre bord car sinon ça aurait pu être cool).
Marquez par cet événement inattendu, les partis se sont alors organisés pour endiguer cette situation. La réponse trouvée fut d'organiser des primaires en amont de l'élection officielle. L'idée est de réduire ainsi les candidatures divergentes mais proches en faisant une pré-sélection en interne afin de présenter un candidat porté par une tendance politique unie! Hélas, on n'est pas doué à ce jour. On l'a vu lors de la primaire socialiste de 2012, lors de la présidence de l'UMP, lors de la primaire socialiste et de droite de 2017. Lors des campagnes pour les primaires, on se met tellement sur la gueule qu'au final, il est relativement compliqué de nous rabibocher après. Alors on peut se mettre en mode "suiveur" car on a perdu mais on n'est pas aussi impliqué et uni que cela. Et au final, je juge que les primaires font plus de mal à notre famille politique que si c'était nommé. Ok, on sera frustré si notre poulain n'est pas choisi et on gueulera contre le président du parti et les instances dirigeante et d'investiture mais au moins, il n'y a pas cette campagne de guerre, de dénigrement, etc. Donc pour moi, les primaires, bien que créées en réponse au vote utile et à l'éparpillement des voix, ne sont absolument pas la solution.
Bien qu'une infamie, aujourd'hui, je ne peux qu'appeler à voter utile pour les élections de 2017. Je sais que Fillon a de nombreuses casseroles mais je ne vote pas pour un saint, je vote pour un programme. Et celui de François Fillon est celui qui me correspond le plus. Je peux être déçu par l'homme, mais il est hors de question pour moi d'aller me rabattre sur des petits partis comme Debout la France. J'ai toute la sympathie du monde pour Nicolas Dupont-Aignan mais voter pour lui, c'est retirer une voix à Fillon. Or le duel sera très serré pour le second tour et je ne veux pas pénaliser ma tendance politique. Me retrouver avec un duel Marine Lepen - Jean-Luc Mélenchon ou Marine Lepen - Emmanuelle Macron, très peu pour moi! Si la France continue encore 5 ans dans ces dérives, on ne s'en relèvera pas. Il faut des reformes profondes. Si vous avez des valeurs de droite, ne vous abstenez pas, ne votez pas pour un petit parti, votez pour le seul qui a les capacités d'être élu et qui est de votre bord. C'est le seul moyen pour que votre tendance politique soit représentée au second tour. C'est triste...mais le système est ainsi fait.
26 Mar
2017
 Par Yann Bidon
Par Yann Bidon
Initiation au jeu de Nim
J’ai envie de débuter une série d’articles sur la théorie des jeux. C’est un domaine particulièrement intéressant des mathématiques et surement un des plus ludiques. Je vous propose de démarrer par une catégorie extrêmement simple de jeux qu’on appelle couramment les jeux de Nim.
Pour ceux qui l’ignorent, les jeux de Nim sont une catégorie de jeux où deux joueurs s’affrontent au tour par tour et qui consistent à prendre ou déplacer des objets en respectant certaines règles pour passer d’un état à un autre (sans avoir la capacité de revenir à un état précédent) jusqu’à atteindre une position de victoire. Cela a l’air assez flou comme ça, n’est-ce pas ? C’est normal, c’est une définition générique car les jeux de Nim englobent un nombre de jeux assez large même si derrière, il y a toujours la même logique. Un des jeux de Nim les plus connus a été rendu populaire à notre époque par une épreuve de Fort Boyard, celle des bâtonnets. Deux joueurs ont devant eux un plateau où se tient un certain nombre de bâtonnets. À chaque tour, le joueur a la capacité de retirer un, deux ou trois bâtonnets. Celui qui retire le dernier bâtonnet a perdu. Ceci est un jeu de Nim, on a deux joueurs qui alternent, chacun peut retirer un certain nombre d’objets fixé par les règles initiales et on arrive à une situation finale qui est de vider le plateau tout en sachant que celui qui prend le dernier perd. En outre, il est impossible de retourner à un état précédent car on ne peut que retirer des bâtonnets. À l’inverse, les échecs par exemple ne sont pas un jeu de Nim car on peut totalement revenir à une position antécédente. Par exemple, je bouge mon cavalier, mon adversaire fait de même puis je remets mon cavalier à sa place initiale et mon adversaire fait de même. Ici, on vient de passer d’un état de l’échiquier à un autre strictement identique. Cela signifie que tout ce qu’on va voir pour être sûr de gagner dans un jeu de Nim ne peut pas s’appliquer dans un jeu d’échec.
Je me dois également de préciser certaines caractéristiques inhérentes au jeu de Nim. Il n’y a pas, dans un jeu de Nim, de notion de hasard. Si je prends l’ensemble des jeux avec des dés par exemple, tel que les petits chevaux, ce ne sont pas des jeux de Nim. C’est également un jeu qui se doit d’avoir ce qu’on appelle des informations complètes et parfaites. Cela signifie qu’on connait exactement l’ensemble des variables qui constituent le jeu. Dans mon jeu des bâtonnets, je vois combien de bâtonnets au total et je sais combien moi et mon adversaire avons la capacité de retirer. À l’inverse, la plupart des jeux de cartes ne sont pas des jeux de Nim tel que le Black Jack ou le Poker car nos informations ne sont pas complètes et parfaites tant on ignore la main de nos adversaires. Là encore, pour ces jeux, c’est d’autres stratégies qu’il va falloir adopter que celle du jeu de Nim. Enfin, un jeu de Nim est un jeu à somme nulle. Cela signifie que si je gagne une manche alors l’autre joueur en perd obligatoire une. Il n’y pas de situations où tout le monde est vainqueur ou perdant. Vous notez que tout ça est assez restrictif mais c’est normal, on a dit qu’on commençait simple. On ne va pas se lancer dans des probabilités ou des graphes à circuits.
Dans tout jeu de Nim, la stratégie est la suivante. La phase la plus complexe est la première, il va falloir lister l’ensemble de tous les états possibles du jeu. En un sens, ce n’est pas difficile, c’est juste long et rébarbatif. Après, on a des ordinateurs pour faire ça maintenant. Ensuite, on tisse les liens qui, en fonction des règles, nous permette de passer d’un état à l’autre. Imaginons dans notre jeu des bâtonnets (qui se fait très bien avec des allumettes aussi), on commence avec 12 éléments alignés. On a donc une liste décroissante de 12 à 1 et comme on peut retirer un, deux ou trois à chaque tour, alors chaque élément est lié à son élément-1, élément-2 et élément-3. Cela nous donne le graphe orienté suivant :
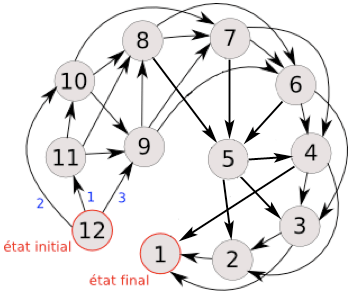
Une fois le graphe fait, vous venez de faire le plus dur du travail. Maintenant, il faut déterminer les états finaux. Dans le cas de notre jeu de bâtonnets, il n’y en a qu’un. C’est quand il en reste plus qu’un. En effet, si on arrive à la fin de notre tour au cas où il n’en reste plus qu’un, on a gagné car l’autre n’a d’autre choix que de le retirer. Mais dans d’autres jeux de Nim, il peut y avoir plusieurs états gagnants. Le but est de les répertorier. À partir de là, on va voir tous les états qui pointent sur eux. Dans notre cas, par exemple, on a le 2, 3 et 4. Ces cas sont considérés comme perdants. Pourquoi ? Car si à la fin de votre tour, vous atterrissez sur un de ces états, votre adversaire peut atteindre la position gagnante et donc vous perdez. On ne veut pas ça. Par contre, c’est tout le sort qu’on souhaite à notre adversaire. C’est pour ça que nous allons chercher un état qui ne mène qu’à des états perdants. Est-ce qu’on a cela ? 5 mène à 2, 3 et 4 qui sont tous perdants. Ainsi, si j’arrivais sur 5, mon adversaire n’aurait d’autres possibilités que de venir sur un état perdant. On dit que 5 est un état gagnant. Et comme 5 est un état gagnant, on reproduit le même processus qu’avec 1. Les états qui pointent dessus sont déclarés perdants et on cherche un état qui pointe que sur des perdants. Il devient un nouveau gagnant et on continue jusqu’à arriver à l’état initial. Ces éléments gagnant sont appelés noyaux. Dans notre cas, on arrive au résultat suivant :
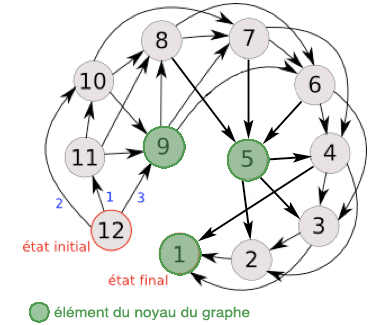
Comme notre logique est bien faite, on note que les éléments du noyau peuvent être tous atteint en deux tours. C’est trivial vu que les perdants pointent forcément sur un gagnant et qu’un gagnant ne pointe que sur des perdants. Ainsi, si à la fin de votre tour, vous arrivez sur une situation gagnante, alors vous êtes sûr de gagner si vous jouez bien. Votre adversaire n’ayant pas le choix de tomber sur un cas perdant, vous devrez alors rejoindre le prochain cas gagnant. Si votre êtes sur 9 et que votre adversaire en retire 3 et atterrit donc sur 6, n’allez pas sur 4 mais sur 5. De même, si vous commencez, allez vite en 9 en en retirant 3.
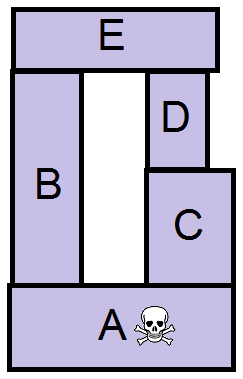
Ainsi, les jeux de Nim ne sont guère intéressants si on joue avec des personnes éclairées car dès le début, vous pouvez savoir qui a gagné ou perdu. Je prends par exemple, le morpion ou tic-tac-toe, je pense qu’on y a tous joué étant enfant. Une fois qu’on sait bien y jouer, au bout du second coup, on sait si on gagne ou si on fait un match nul (si le joueur joue bien, car sinon, il peut commettre des erreurs et on peut les exploiter pour gagner). Après, bien que déterminable, on ne s’amuse pas toujours à calculer les noyaux d’un graphe dans notre tête. Car créer le graphe peut s’avérer parfois complexe bien que possible. Par exemple, si je prends le puissance 4, le nombre de configuration possible est énorme. Mais on peut le faire (ce qui me permet de vous dire que si deux joueurs jouent parfaitement au puissance 4, si le premier joueur met son pion au milieu, il est assuré de gagner et à l'inverse s'il le met sur les extrémités, il est assuré de perdre). Malgré tout, sur les Nim, cette stratégie marche toujours. Je vous laisse l’essayer sur ce petit jeu. Vous et votre adversaire vous retrouvez devant cette pile. À chaque tour, vous devez retirer un morceau. Attention toutefois, Si vous prenez une pièce, vous êtes obligé de prendre toutes les pièces qui sont au-dessus de celle-ci. Celui qui prend le dernier morceau avec le crane a perdu. Vous débutez, quelle pièce devez-vous prendre ?
12 Mar
2017
 Par Yann Bidon
Par Yann Bidon
Que faire à la création d'un projet
Bonjour à toutes et à tous,
On a une idée et souhaite la concrétiser. On va alors mettre un place un projet pour cela. Mais il convient de se poser des questions essentielles en amont pour déterminer s'il est opportun de lancer ce projet. Ces dernières vont vous être présenté en détail dans cette vidéo.
Quel est le besoin auquel doit répondre votre projet? Quels sont vos objectifs et vos attendus? Quels sont les ressources nécessaires au bon déroulé du projets? Quels sont les risques que je peux rencontrer? Voilà tant de questions qu'il faut impérativement se poser et y répondre le plus clairement possible lors de la création d'un projet.
<youtube>SX2bTW4xe20
18 Feb
2017
 Par Yann Bidon
Par Yann Bidon
D'où vient le discriminant et son utilité?
J'imagine qu'on a déjà dû vous apprendre à résoudre une équation du second degré, sinon vous ne chercherez pas un article sur le discriminant en mathématique. On a dû vous expliquer que lorsqu'on avait un polynôme du second degré, du type [math]ax^2+bx+c[/math] et que vous recherchez les racines, c'est-à-dire lorsque ce polynôme s'annule, on cherche un delta majuscule qu'on appelle Discriminant tel que [math]\Delta = b^2 - 4ac[/math] et on regarde son signe. Alors, on gobe ça, ça marche très bien mais on ne nous explique pas toujours d'où il vient. Pourquoi cette valeur [math]b^2 - 4ac[/math] ? Cela sort d'où? Et en quoi son signe nous permet de déterminer les racines d'un polynôme?
Je ne sais pas vous mais personnellement, je n'aime pas apprendre bêtement des choses. J'ai besoin de comprendre. Une fois que j'ai assimilé la logique, je retiens beaucoup plus facilement que du par-cœur car du coup, ça fait sens. Bien sûr, ce n'est pas un savoir caché et certains professeurs l'expliquent et c'est génial. Mais avec la pression du programme et le peu de temps qu'on a pour le faire, certains ont tendance à aller à l'essentiel en donnant les outils sans mentionner pourquoi ils marchent. En réalité, il nous appartient à nous de chercher et une simple recherche sur le net vous amènera la réponse. C'est peut-être même ça qui vous a amené. Donc rentrons dans le vif du sujet.
Pour vous montrer que c'est absolu, générique, je ne vais pas prendre un exemple spécifique et je vais rester avec la fonction [math]f(x) = ax^2+bx+c[/math]. L'idée va être de réécrire cette fonction sous une autre forme. Cette nouvelle forme s'appelle la forme canonique. Tout d'abord, on va factoriser a : [math]ax^2+bx+c = a(x^2+ \frac{b}{a}x + \frac{c}{a})[/math]. Jusque là, ça ne casse pas trois pattes à un canard. Ensuite, c'est là que se passe toute l'intelligence du processus. On note qu'on a presque une identité remarquable. Effectivement, [math](x + \frac{b}{2a})^2 = x^2 + \frac{b}{a}x + (\frac{b}{2a})^2[/math]. On y est presque dans notre cas. Il nous manque juste [math](\frac{b}{2a})^2[/math]. Dans notre polynôme factorisé, on peut ajouter 0 sans rien changer du résultat, vous êtes d'accord? [math]a(x^2+ \frac{b}{a}x + \frac{c}{a}) = a(x^2+ \frac{b}{a}x + 0 + \frac{c}{a})[/math]. Mais pourquoi écrire bêtement 0 lorsqu'on peut écrire [math](\frac{b}{2a})^2 - (\frac{b}{2a})^2[/math]  ? Notre fonction devient [math]f(x) = a(x^2+ \frac{b}{a}x + (\frac{b}{2a})^2 - (\frac{b}{2a})^2 + \frac{c}{a})[/math]. On s'est embêté à retrouver une identité remarquable donc utilisons la : [math]f(x) = a((x +\frac{b}{2a})^2 - (\frac{b}{2a})^2 + \frac{c}{a})[/math]. Bien, on a un carré, l'avantage est qu'on sait que ça sera toujours positif ou nul.
? Notre fonction devient [math]f(x) = a(x^2+ \frac{b}{a}x + (\frac{b}{2a})^2 - (\frac{b}{2a})^2 + \frac{c}{a})[/math]. On s'est embêté à retrouver une identité remarquable donc utilisons la : [math]f(x) = a((x +\frac{b}{2a})^2 - (\frac{b}{2a})^2 + \frac{c}{a})[/math]. Bien, on a un carré, l'avantage est qu'on sait que ça sera toujours positif ou nul.
Maintenant, intéressons-nous à ce qu'il reste. On va notamment les mettre sous le même dénominateur : [math] - (\frac{b}{2a})^2 + \frac{c}{a} = -\frac{b^2}{4a^2} + \frac{c}{a} = \frac{-b^2}{4a^2} + \frac{4ac}{4a^2} = \frac{-b^2 + 4ac}{4a^2} = - \frac{b^2 - 4ac}{4a^2}[/math]. Remettons cela dans notre fonction, on finit avec : [math]f(x) = a((x +\frac{b}{2a})^2 - \frac{b^2 - 4ac}{4a^2})[/math].
Je rappelle le but initial, c'est de trouver pour quel x, on a [math]f(x) = 0[/math]. Donc [math]f(x) = 0 \Rightarrow a((x +\frac{b}{2a})^2 - \frac{b^2 - 4ac}{4a^2}) = 0 \Rightarrow (x +\frac{b}{2a})^2 - \frac{b^2 - 4ac}{4a^2} = 0\Rightarrow (x +\frac{b}{2a})^2 = \frac{b^2 - 4ac}{4a^2}[/math]. On arrive donc à un carré qui doit être égal à un nombre de signe variable. Mais de quoi dépend réellement le signe de ce nombre? De [math]4a^2[/math]? Évidemment que non car a au carré sera toujours positif donc [math]4a^2[/math] aussi. La seule chose qui va faire influer le résultat est le signe de [math]b^2 - 4ac[/math]. Et comme on a la flemme de réécrire ça à chaque fois, on a dit qu'on allait créer une variable pour ça, et on a établi que [math]\Delta = b^2 - 4ac[/math].
Force est de constater qu'on retrouve ici notre discriminant et qu'au final, tout dépend de lui pour trouver l'égalité qui permet de déterminer les x tel que f(x) = 0. Pour être plus précis, tout dépend du signe du discriminant donc travaillons par disjonction des cas.
Si [math]\Delta > 0[/math]
Un carré est égal à un nombre positif. Cela signifie qu'on peut appliquer de part et d'autres de l'équation la fonction racine carrée définie sur [math][0;+\infty[[/math]. On a donc [math](x +\frac{b}{2a})^2 = \frac{\Delta}{4a^2}[/math] [math]\Rightarrow x +\frac{b}{2a} = \sqrt{\frac{\Delta}{4a^2}}\Rightarrow x +\frac{b}{2a} = |\frac{\sqrt{\Delta}}{2a}|[/math].
Ainsi, on arrive à deux cas: [math]x +\frac{b}{2a} = \frac{\sqrt{\Delta}}{2a}\Rightarrow x = \frac{-b+\sqrt{\Delta}}{2a}[/math] et [math]x +\frac{b}{2a} = - \frac{\sqrt{\Delta}}{2a}\Rightarrow x = \frac{-b-\sqrt{\Delta}}{2a}[/math].
Si [math]\Delta = 0[/math]
C'est le cas le plus simple car du coup, [math]\frac{\Delta}{4a^2} = 0[/math]. On se retrouve ainsi avec [math](x +\frac{b}{2a})^2 = 0 \Rightarrow x +\frac{b}{2a} = 0 \Rightarrow x = -\frac{b}{2a}[/math].
Si [math]\Delta < 0[/math]
Dans les réels, un carré ne peut pas égaler un nombre négatif. On s'arrête donc là, il n'y a pas de solution. Point.
Après, ça, c'est dans les réels. Mais pourquoi se borner à cela? On pose [math] -1 = i^2[/math] et nous voici dans les complexes. Or [math]\Delta < 0 \Rightarrow -1 \times \Delta > 0 \Rightarrow i^2 \times \Delta > 0 [/math].
En réécrivant notre delta avec i au carré, on se retrouve donc avec un nombre positif. On n'a donc plus qu'à appliquer le raisonnement vu avec delta positif et on tombe sur : [math]x +\frac{b}{2a} = \frac{\sqrt{\Delta i^2}}{2a}\Rightarrow x = \frac{-b+\sqrt{\Delta}i}{2a}[/math] et [math]x +\frac{b}{2a} = - \frac{\sqrt{\Delta i^2}}{2a}\Rightarrow x = \frac{-b-\sqrt{\Delta}i}{2a}[/math].
Voilà, maintenant, le discriminant n'a plus de secrets pour vous. Vous savez d'où il vient et pourquoi son signe vous donne tant d'informations pour déterminer les racines.
25 Jan
2017
 Par Yann Bidon
Par Yann Bidon
Et si l'Assemblée Nationale tombait?
L'Assemblée Nationale représente avec le Sénat le pouvoir législatif. Cela signifie qu'ils leur reviennent d'élaborer, proposer et voter des lois et de gérer le budget. En théorie, sans ce pouvoir, il n'y a pas de nouvelles lois car toute loi doit être votée par le Parlement. Il est possible, dans le cas des ordonnances, de mettre en application directement la loi sans attendre qu'elle soit votée mais quoiqu'il arrive, elle devra à un moment ou à un autre être votée par le Parlement. Au sein du Parlement, le dernier mot revient à l'Assemblée Nationale, qui représente les citoyens français (le Sénat représentant les collectivités locales).
Du coup, force est de constater que c'est une instance relativement importante. Que se passerait-il si cette dernière serait incapable de se réunir ou serait dissoute illégalement? Cela peut arriver. Imaginez que les parisiens se révoltent, ou bien qu'on se fasse envahir et que l'ennemi assiège Paris ou pire, un dictateur abuse de son pouvoir de président et dissout l'Assemblée plusieurs fois sans attendre la période légale prévue dans la loi ou bien qu'un coup d'État se déclenche. Les possibilités sont nombreuses. Alors tout d'un coup, tout l'appareil législative s'arrête? Plus aucune règle nationale ne peut se déclencher et seules les arrêtés des collectivités locales et les ordonnances permettraient de créer un peu d'ordre?
Heureusement, notre loi a prévu ce scénario et a prévu un plan d'action si cela devait arriver. Et il faut dire qu'elle l'a prévu de longue date car la Loi Tréveneuc date du 15 février 1872. Elle a été faite sous la IIIe République et contrairement à ce qu'on pourrait intuitivement croire, elle est toujours appliquée et appliquable. Pour remettre un peu de contexte, en 1870, une guerre éclate entre d'un côté le Second Empire français de Napoléon III et une coalition mené par la Prusse et composé d'États allemandes comme la confédération d'Allemagne du Nord, le royaume de Bavière et le Grand-Duché de Bade. Mais vous voulez connaître le pire? Le Pire?! On a perdu  . Ils nous prendront l'Alsace et la Moselle en plus de détruire le Second Empire. Et vous savez pourquoi?! Parce qu'on n'était pas prêt! Et le comble est que c'est nous qui avions déclaré la guerre (car on ne voulait pas qu'un prince prussien soit en lice pour le trône d'Espagne et que la France se trouve prise en étau). Bref, comment cela s'est-il passé? On n'était pas de taille, la France n'a pas su mobiliser, ils ont assiégé Paris et l'ont surtout encerclé de sorte que plus rien ne sorte. Et du coup, toutes les provinces étaient séparées du pouvoir central et donc du commandement. Et cela joua en faveur de l'ennemi. Et l'on perdit.
. Ils nous prendront l'Alsace et la Moselle en plus de détruire le Second Empire. Et vous savez pourquoi?! Parce qu'on n'était pas prêt! Et le comble est que c'est nous qui avions déclaré la guerre (car on ne voulait pas qu'un prince prussien soit en lice pour le trône d'Espagne et que la France se trouve prise en étau). Bref, comment cela s'est-il passé? On n'était pas de taille, la France n'a pas su mobiliser, ils ont assiégé Paris et l'ont surtout encerclé de sorte que plus rien ne sorte. Et du coup, toutes les provinces étaient séparées du pouvoir central et donc du commandement. Et cela joua en faveur de l'ennemi. Et l'on perdit.
Traumatisée par ce passif douloureux, l'Assemblée Nationale vote la loi Tréveneuc. Celle-ci prévoit qu'en cas de dissolution illégale de l'Assemblée Nationale ou d'impossibilité de se réunir, les conseils généraux (aujourd'hui, les conseils départementaux et métropolitains) doivent se saisir et se réunir au chef lieu du département ou, en cas d'impossibilité, dans n'importe quel lieu du département, pour désigner deux délégués en comité secret. Pour que cette élection soit valide, il faut que plus de la moitié du conseil soit présent. Ces deux délégués doivent alors rejoindre un lieu de regroupement avec les membres du gouvernement et les députés qui ont su s'échapper de Paris à temps. De là, une nouvelle assemblée nommée Assemblée des délégués se charge de reprendre le rôle de l'Assemblée Nationale. Le temps que cette assemblée des délégués se forme, les conseils départementaux et métropolitains ont tout pouvoir pour assurer l'ordre et le maintien de la tranquillité publique.
L'ensemble du corps d'État et donc l'ensemble des fonctionnaires et notamment les armées sont assujettis aux décisions de cette assemblée sous peine de forfaiture (et donc de trahison). Toutefois, dès que l'Assemblée Nationale pourra de nouveau être normalement constituée, l'assemblée des délégués se doit impérativement d'être dissoute au profit de l'authentique, de la seule et unique Assemblée Nationale. Si, au bout d'un mois, ce n'est toujours pas le cas, des élections départementales et métropolitaines doivent être organisé.


